题目内容
15．某颜料公司生产A、B两种产品，其中生产每吨A产品，需要甲染料1吨，乙染料4吨，丙染料2吨；生产每吨B产品，需要甲染料1吨，乙染料0吨，丙染料5吨，且该公司一天之内甲、乙、丙三种染料的用量分别不超过50吨、160吨、200吨．如果A产品的利润为300元/吨，B产品的利润为200元/吨，则该颜料公司一天内可获得的最大利润为（ ）| A． | 14000元 | B． | 16000元 | C． | 18000元 | D． | 20000元 |
分析 列出约束条件，再根据约束条件画出可行域，再利用利润z=300x+200y的几何意义求最值即可．
解答 
解：设生产A产品x吨，B产品y吨，则$\left\{\begin{array}{l}{x+y≤50}\\{4x≤160}\\{2x+5y≤200}\\{x，y∈N}\end{array}\right.$
（x，y∈N）
利润z=300x+200y，
可行域如图所示，由$\left\{\begin{array}{l}{4x=160}\\{x+y=50}\end{array}\right.$，可得x=40，y=10，
结合图形可得x=40，y=10时，zmax=14000．
故选：A．
点评 本题考查了列一元一次不等式组解实际问题的运用及一元一次不等式组的解法的运用，解答时找到题意中的不相等关系是建立不等式组的关键．
练习册系列答案
阅读快车系列答案
相关题目
5．执行如图所示的程序框图，若输入的n=5，则输出的结果为（ ）
| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
6．已知tanα=$\frac{3}{4}$，则sin2α=（ ）
| A． | $-\frac{12}{25}$ | B． | $\frac{12}{25}$ | C． | $-\frac{24}{25}$ | D． | $\frac{24}{25}$ |
10．已知数列{an}满足：a1=1，an+1=$\frac{a_n}{{{a_n}+2}}$（n∈N*）若${b_{n+1}}=（n-2λ）•（\frac{1}{a_n}+1）$（n∈N*），b1=-$\frac{3}{2}$λ，且数列{bn}是单调递增数列，则实数λ的取值范围是（ ）
| A． | $λ＜\frac{4}{5}$ | B． | λ＜1 | C． | $λ＜\frac{3}{2}$ | D． | $λ＜\frac{2}{3}$ |
20．执行如图所示的程序框图，输出s的值为（ ）
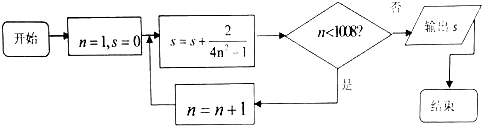
| A． | 1 | B． | $\frac{2018}{2019}$ | C． | $\frac{2018}{2017}$ | D． | $\frac{2016}{2017}$ |
7．已知函数f（x）=lnx+x，则曲线f（x）在点P（1，f（1））处的切线与两坐标轴围成的三角形的面积为（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | 1 | D． | 2 |
4．已知复数2i-3是方程2x2+px+q=0的一个根，则实数p，q的值分别是（ ）
| A． | 12，0 | B． | 24，26 | C． | 12，26 | D． | 6，8 |