题目内容
某工厂分别生产甲、乙两种产品1箱时所需要的煤、电以及获得的纯利润如下表所示.
若生产甲、乙两种产品可使用的煤不超过120吨,电不超过60千度,则可获得的最大纯利润和是( )
| 煤(吨) | 电(千度) | 纯利润(万元) | |
| 1箱甲产品 | 3 | 1 | 2 |
| 1箱乙产品 | 1 | 1 | 1 |
| A、60万元 | B、80万元 |
| C、90万元 | D、100万元 |
考点:简单线性规划的应用,简单线性规划
专题:不等式的解法及应用
分析:求得线性约束条件
,目标函数为z=2x+y,作出可行域,根据图象即可求得结论.
|
解答:
解:设每天生产甲种产品x箱,乙种产品y箱.
依题意可得线性约束条件
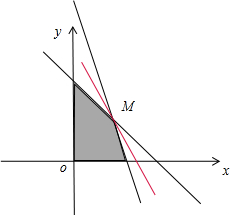
目标函数为z=2x+y,…(7分)
作出线性约束条件所表示的平面区域如图所示.
将z=2x+y变形为y=-2x+z
当直线y=-2x+z
在纵轴上的截距z达到最大值时,
即直线y=-2x+z经过点M时,z也达到最大值.
由
得M点的坐标为(30,30)
∴当x=30,y=30时,zmax=2×30+30=90
因此,该厂每天生产甲种产品30箱,乙种产品30箱,才能使该厂日产值最大,最大的产值是90万元.
故选:C.
依题意可得线性约束条件
|

目标函数为z=2x+y,…(7分)
作出线性约束条件所表示的平面区域如图所示.
将z=2x+y变形为y=-2x+z
当直线y=-2x+z
在纵轴上的截距z达到最大值时,
即直线y=-2x+z经过点M时,z也达到最大值.
由
|
∴当x=30,y=30时,zmax=2×30+30=90
因此,该厂每天生产甲种产品30箱,乙种产品30箱,才能使该厂日产值最大,最大的产值是90万元.
故选:C.
点评:本题考查线性规划知识的运用,考查数形结合的数学思想,考查学生利用数学知识解决实际问题的能力,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
,则下列结论中正确的是( )
| sin(x+π) |
| cos(π-x) |
| A、f(x)的最小正周期是2π | ||
| B、f(x)在[4,5]上单调递增 | ||
C、f(x)的图象关于x=
| ||
D、f(x)的图象关于点(
|
已知集合A={0,1,2,3,4},集合B={0,2,4,6,8},则A∩B=( )
| A、{0} |
| B、{0,4} |
| C、{2,4} |
| D、{0,2,4} |
在平行四边形ABCD中,
=
,
=
,
=3
,M为BC的中点,则
=( )
| AB |
| a |
| AD |
| b |
| AN |
| NC |
| MN |
A、-
| ||||||||
B、-
| ||||||||
C、
| ||||||||
D、-
|
某班有60名学生,其中正、副班长各1人,现要选派5人参加一项社区活动,要求正、副班长至少1人参加,问共有多少种选派方法?下面是学生提供的四个计算式,其中错误的是( )
A、C
| ||||||||
B、C
| ||||||||
C、C
| ||||||||
D、C
|
设全集U={3,4,5,6},集合A={3,5,6},B={4,5,6},则∁UA∩B=( )
| A、{4,7} | B、{3,6} |
| C、{4} | D、{7} |
设复数z满足z•(i-1)=2i(其中i为虚数单位),则z等于( )
| A、1-i | B、1+i |
| C、-1+i | D、-1-i |