题目内容
函数y=2+
sinx的最小正周期和最小值分别为( )
| 2 |
| A、π,1 | ||
| B、2π,1 | ||
C、π,2-
| ||
D、2π,2-
|
考点:三角函数的周期性及其求法,正弦函数的定义域和值域
专题:三角函数的图像与性质
分析:根据函数的解析式求出函数的周期性和最值.
解答:
解:∵函数y=2+
sinx的最小正周期为2π,当sinx=-1时,函数取得最小值为2-
,
故选:D.
| 2 |
| 2 |
故选:D.
点评:本题主要考查三角函数的周期性和最值,属于基础题.

练习册系列答案
相关题目
已知y=sin(π+x)-cos2x,则y的最小值和最大值分别为( )
A、-
| ||
B、-2,
| ||
C、-
| ||
D、-2,
|
已知函数f(x)=
,则下列结论中正确的是( )
| sin(x+π) |
| cos(π-x) |
| A、f(x)的最小正周期是2π | ||
| B、f(x)在[4,5]上单调递增 | ||
C、f(x)的图象关于x=
| ||
D、f(x)的图象关于点(
|
已知集合A={0,1,2,3,4},集合B={0,2,4,6,8},则A∩B=( )
| A、{0} |
| B、{0,4} |
| C、{2,4} |
| D、{0,2,4} |
设复数z满足z•(i-1)=2i(其中i为虚数单位),则z等于( )
| A、1-i | B、1+i |
| C、-1+i | D、-1-i |
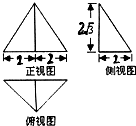 一个几何体的三视图如图所示,其中正视图是正三角形,则该几何体的三个侧棱与地面所成的角的集合为
一个几何体的三视图如图所示,其中正视图是正三角形,则该几何体的三个侧棱与地面所成的角的集合为