题目内容
6.已知$|{\vec a}|=1$,$|{\vec b}|=2$,$\vec a(\vec a-\vec b)=3$则$\vec a$与$\vec b$的夹角为( )| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{2}$ | D. | π |
分析 根据平面向量数量积的定义,即可求出$\vec a$与$\vec b$的夹角大小.
解答 解:设$\vec a$与$\vec b$的夹角为θ,$|{\vec a}|=1$,$|{\vec b}|=2$,
∵$\overrightarrow{a}$•($\overrightarrow{a}$-$\overrightarrow{b}$)=${\overrightarrow{a}}^{2}$-$\overrightarrow{a}$•$\overrightarrow{b}$=12-1×2×cosθ=3,
∴cosθ=1;
又θ∈[0,π],
∴$\vec a$与$\vec b$的夹角为π.
故选:D.
点评 本题考查了平面向量数量积的定义与应用问题,是基础题目.

练习册系列答案
相关题目
16.已知a=cos17°cos23°-sin17°sin23°,b=2cos225°-1,c=$\frac{{\sqrt{3}}}{2}$,则a,b,c的大小关系( )
| A. | b>a>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
18.已知a=cos61°•cos127°+cos29°•cos37°,$b=\frac{{2tan{{13}°}}}{{1+{{tan}^2}{{13}°}}}$,$c=\sqrt{\frac{{1-cos{{50}°}}}{2}}$,则a,b,c的大小关系是( )
| A. | a<b<c | B. | a>b>c | C. | c>a>b | D. | a<c<b |
15.将函数y=cos(2x+φ)的图象向右平移$\frac{π}{3}$个单位,得到的函数为奇函数,则|φ|的最小值( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
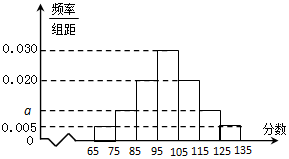 某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图:
某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图: