题目内容
圆(x-1)2+y2=4内有一点P(1,1),AB过点P.
(1)若弦长|AB|=2
,求直线AB的斜率;
(2)若圆上恰有三点到直线AB的距离等于l,求直线AB的方程.
(1)若弦长|AB|=2
| 3 |
(2)若圆上恰有三点到直线AB的距离等于l,求直线AB的方程.
考点:直线与圆相交的性质
专题:综合题,直线与圆
分析:(1)由弦长公式求出圆心到直线AB的距离,点斜式设出直线方程,由点到直线的距离公式求出斜率;
(2)由题意知,圆心到直线AB的距离d=1,由(1)知k=0或-
,从而可求直线AB的方程.
(2)由题意知,圆心到直线AB的距离d=1,由(1)知k=0或-
| 4 |
| 3 |
解答:
解:(1)设圆心(1,0)到直线AB的距离为d,则d=
=1,
设直线AB的斜率为k,则直线AB的方程y-1=k(x+1),即kx-y+k+1=0,
∴d=1=
,
∴k=0或-
.
(2)∵圆上恰有三点到直线AB的距离等于1,
∴圆心(-1,0)到直线AB的距离d=1,
由(1)知k=0或-
,
∴直线AB的方程y=1或4x+3y+1=0.
| 4-3 |
设直线AB的斜率为k,则直线AB的方程y-1=k(x+1),即kx-y+k+1=0,
∴d=1=
| |2k+1| | ||
|
∴k=0或-
| 4 |
| 3 |
(2)∵圆上恰有三点到直线AB的距离等于1,
∴圆心(-1,0)到直线AB的距离d=1,
由(1)知k=0或-
| 4 |
| 3 |
∴直线AB的方程y=1或4x+3y+1=0.
点评:本题考查弦长公式、点到直线的距离公式的应用,及用待定系数法求直线的斜率、直线方程.

练习册系列答案
相关题目
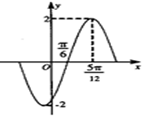 已知函数f(x)=Msin(ωx+φ)(x∈R,M>0,ω>0,|φ|<
已知函数f(x)=Msin(ωx+φ)(x∈R,M>0,ω>0,|φ|<