题目内容
已知双曲线
-
=1（a＞0，b＞0）左，右焦点分别为F1、F2．若在双曲线右支上存在一点P使|PF1|=4|PF2|，则双曲线离心率e的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、（1，
| ||
| B、（1，2] | ||
C、[
| ||
D、[
|
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：由双曲线的定义可得|PF1|-|PF2|=3|PF2|=2a，再根据点P在双曲线的右支上，可得|PF2|≥c-a，从而求得此双曲线的离心率e的取值范围．
解答：
解：∵|PF1|=4|PF2|，
∴由双曲线的定义可得|PF1|-|PF2|=3|PF2|=2a，
∴|PF2|=
，
∵点P在双曲线的右支上，
∴|PF2|≥c-a，
∴
≥c-a，
∴e=
≤
，
∵e＞1，
∴1＜e≤
，
∴双曲线的离心率e的取值范围为（1，
]．
故选：A．
∴由双曲线的定义可得|PF1|-|PF2|=3|PF2|=2a，
∴|PF2|=
| 2a |
| 3 |
∵点P在双曲线的右支上，
∴|PF2|≥c-a，
∴
| 2a |
| 3 |
∴e=
| c |
| a |
| 5 |
| 3 |
∵e＞1，
∴1＜e≤
| 5 |
| 3 |
∴双曲线的离心率e的取值范围为（1，
| 5 |
| 3 |
故选：A．
点评：本题考查双曲线的定义和标准方程，以及双曲线的简单性质的应用，考查学生的计算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
极坐标方程（ρ-1）θ=0（ρ≥0）表示的曲线是（ ）
| A、圆 | B、直线 |
| C、圆和直线 | D、圆和射线 |
在极坐标系中，过点A（1，0）且垂直于极轴的直线的极坐标方程为（ ）
| A、ρ=sinθ |
| B、ρ=1 |
| C、ρcosθ=1 |
| D、ρsinθ=1 |
设集合P={x∈R|x2+2x＜0}，Q={x∈R|
＞0}，则P∩Q=（ ）
| 1 |
| x+1 |
| A、（-2，1） | B、（-1，0） |
| C、∅ | D、（-2，0） |
下列函数在其定义域内不是连续函数的是（ ）
| A、y=x3 | ||
| B、y=|x-1| | ||
C、y=
| ||
D、y=
|
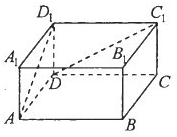如图，在长方体ABCD-A1B1C1D1中，底面是边长为2的正方形，高为1，则异面直线AD1和DC1所成角的余弦值等于（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
一次调查男女学生喜欢语文学科情况，共调查了90人，具体如下：据此材料，你认为喜欢语文学科与性别（ ）
| 喜欢 | 不喜欢 | |
| 男 | 20 | 25 |
| 女 | 30 | 15 |
| A、有关 | B、无关 |
| C、不确定 | D、无法判断 |