题目内容
已知命题P:?x∈(0,1),x2<x3;命题q:若函数f(x)=ln(a+
)为奇函数,则a=-1,下列命题中真命题是( )
| 2 |
| x+1 |
| A、p∧q | B、p∧¬q |
| C、¬p∧q | D、¬p∧¬q |
考点:复合命题的真假
专题:阅读型
分析:利用幂函数的单调性与对数函数的奇偶性判定命题p、q的真假,再根据复合命题真值表可得答案.
解答:
解:∵x∈(0,1),x3-x2=x2(x-1)<0,∴x3<x2,
∴命题P为假命题;
函数f(x)=ln(a+
)为奇函数,则f(0)=ln(a+2)=0⇒a+2=1⇒a=-1,
∴命题q为真命题,
根据复合命题真值表知,¬p为真命题,¬p∧q为真命题.
故选:C.
∴命题P为假命题;
函数f(x)=ln(a+
| 2 |
| x+1 |
∴命题q为真命题,
根据复合命题真值表知,¬p为真命题,¬p∧q为真命题.
故选:C.
点评:本题借助考查复合命题的真假判断,考查了对数函数的奇偶性及幂函数的性质,解题的关键是熟练掌握复合命题的真假规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
等比数列{an}的首项1,公比为2,则a4=( )
| A、2 | B、4 | C、8 | D、16 |
极坐标方程(ρ-1)θ=0(ρ≥0)表示的曲线是( )
| A、圆 | B、直线 |
| C、圆和直线 | D、圆和射线 |
在-9和3之间插入n个数,使这n+2个数组成和为-21的等差数列,则n=( )
| A、4 | B、5 | C、6 | D、7 |
从不同号码的三双靴中任取4只,其中恰好有一双的取法种数为( )
| A、12 | B、24 | C、36 | D、72 |
812014除以100的余数是( )
| A、1 | B、79 | C、21 | D、81 |
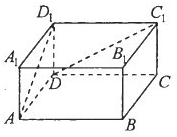 如图,在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为1,则异面直线AD1和DC1所成角的余弦值等于( )
如图,在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为1,则异面直线AD1和DC1所成角的余弦值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、-
|