题目内容
在区域D:(x-1)2+y2≤4内随机取一个点,则此点到点A(1,2)的距离小于2的概率是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
考点:几何概型
专题:计算题,概率与统计
分析:确定满足到点A(1,2)的距离小于2的点的区域,求出其面积,以面积为测度可求概率.
解答:
 解:解:区域D:(x-1)2+y2≤4的面积为4π,满足到点A(1,2)的距离小于2的点在如图阴影部分的区域内.
解:解:区域D:(x-1)2+y2≤4的面积为4π,满足到点A(1,2)的距离小于2的点在如图阴影部分的区域内.
由题意,∠ACB=120°,
∴S阴影=2(
-S△ABC)=2×
-2
,
∴所求概率P=
=
-
.
故选:B.
 解:解:区域D:(x-1)2+y2≤4的面积为4π,满足到点A(1,2)的距离小于2的点在如图阴影部分的区域内.
解:解:区域D:(x-1)2+y2≤4的面积为4π,满足到点A(1,2)的距离小于2的点在如图阴影部分的区域内.由题意,∠ACB=120°,
∴S阴影=2(
| π×22 |
| 3 |
| 4π |
| 3 |
| 3 |
∴所求概率P=
| ||||
| 4π |
| 2 |
| 3 |
| ||
| 2π |
故选:B.
点评:本题考查了几何关系的概率计算,考查图形面积的计算,确定图形的面积是关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
等比数列{an}的首项1,公比为2,则a4=( )
| A、2 | B、4 | C、8 | D、16 |
812014除以100的余数是( )
| A、1 | B、79 | C、21 | D、81 |
如图,正方体ABCD-A′B′C′D′中,E是棱BC的中点,G是棱DD′的中点,则异面直线GB与B′E所成的角为( )

| A、120° | B、90° |
| C、60° | D、30° |
设集合P={x∈R|x2+2x<0},Q={x∈R|
>0},则P∩Q=( )
| 1 |
| x+1 |
| A、(-2,1) | B、(-1,0) |
| C、∅ | D、(-2,0) |
若a<b,则下列不等式中正确的是( )
| A、ac<bc | ||||
B、
| ||||
| C、a-c<b-c | ||||
| D、a+c>b+c |
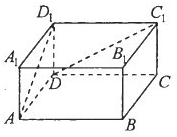 如图,在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为1,则异面直线AD1和DC1所成角的余弦值等于( )
如图,在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为1,则异面直线AD1和DC1所成角的余弦值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
角α的终边过P(sin
,cos
),则角α的最小正值是( )
| 2π |
| 3 |
| 2π |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数y=sinx(x∈R)的图象如图所示,则t的值是( )


A、
| ||
| B、π | ||
C、
| ||
| D、2π |