题目内容
 一个空间几何体的正视图,侧视图,俯视图都为全等的等腰直角三角形(如图所示),如果直角三角形的直角边长为1,那么这个几何体的外接球的体积为( )
一个空间几何体的正视图,侧视图,俯视图都为全等的等腰直角三角形(如图所示),如果直角三角形的直角边长为1,那么这个几何体的外接球的体积为( )| A、3π | ||||
B、
| ||||
| C、12π | ||||
D、
|
考点:球内接多面体,球的体积和表面积
专题:空间位置关系与距离
分析:由三视图知几何体是一个三棱锥,其外接球可以看成是一个棱长为1的正方体的外接球,求出球的半径后,代入球的体积公式,可得答案.
解答:
解:根据三视图,可知该几何体是三棱锥,
下图为该三棱锥的直观图,

由图可知,该几何体的外接球,即为以PA,PB,PC为长宽高的长方体的外接球,
∵PA=PB=PC=1,
故外接球的直径2R=
,
解得R=
,
故这个几何体的外接球的体积V=
πR3=
π,
故选:B
下图为该三棱锥的直观图,

由图可知,该几何体的外接球,即为以PA,PB,PC为长宽高的长方体的外接球,
∵PA=PB=PC=1,
故外接球的直径2R=
| 3 |
解得R=
| ||
| 2 |
故这个几何体的外接球的体积V=
| 4 |
| 3 |
| ||
| 2 |
故选:B
点评:本题考查的知识点是球的体积和表面积,其中根据已知条件求出球的半径是解答本题的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
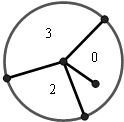 如图所示,旋转一次的圆盘,指针落在圆盘中3分处的概率为a,落在圆盘中2分处的概率为b,落在圆盘中0分处的概率为c,(a,b,c∈(0,1)),已知旋转一次圆盘得分的数学期望为1分,则
如图所示,旋转一次的圆盘,指针落在圆盘中3分处的概率为a,落在圆盘中2分处的概率为b,落在圆盘中0分处的概率为c,(a,b,c∈(0,1)),已知旋转一次圆盘得分的数学期望为1分,则| 2 |
| a |
| 1 |
| 3b |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数y=
sin2x图象的一条对称轴是( )
| 1 |
| 5 |
A、x=-
| ||
B、x=-
| ||
C、x=
| ||
D、x=-
|
下表是甲、乙两个班级进行数学考试,按学生考试及格及不及格统计成绩后的2×2列联表:则X2的值为( )
| 不及格 | 及格 | 合计 | |
| 甲班 | 12 | 33 | 45 |
| 乙班 | 9 | 36 | 45 |
| 合计 | 21 | 69 | 90 |
| A、0.559 | B、0.456 |
| C、0.443 | D、0.4 |
在△ABC中,a,b,c分别为角A,B,C的对边,且(a+b+c)(a-b+c)=3ac,则tanB=( )
A、2+
| ||
B、
| ||
| C、1 | ||
D、2-
|
将正方形ABCD沿对角线BD折成一个直二面角,点C到达点C1,则异面直线AB与C1D所成角是( )
| A、90° | B、60° |
| C、45° | D、30° |
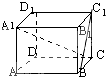 如图,长方体ABCD-A1B1C1D1中,AB=AA1=2BC,则直线BC1与直线A1C所成角的余弦值为( )
如图,长方体ABCD-A1B1C1D1中,AB=AA1=2BC,则直线BC1与直线A1C所成角的余弦值为( )A、-
| ||||
B、
| ||||
C、
| ||||
D、
|
正方体的八个顶点共可以连成28条直线,从这28条直线中任取2条直线,这2条直线恰好是一对异面直线.则这样不同的异面直线有多少对( )
| A、174 | B、87 |
| C、348 | D、84 |