题目内容
设i为虚数单位，复数z的共轭复数为
，且（
-1）（1+i）=2i，则复数z=（ ）
. |
| z |
. |
| z |
| A、2+i | B、2-i |
| C、-2+i | D、-2-i |
考点：复数代数形式的乘除运算
专题：数系的扩充和复数
分析：把给出的等式两边同时乘以
，然后利用复数代数形式的除法运算化简，求得
，则复数z可求．
| 1 |
| 1+i |
. |
| z |
解答：
解：由（
-1）（1+i）=2i，得：
-1=
=
=
=1+i，
∴
=2+i，
则z=2-i．
故选：B．
. |
| z |
. |
| z |
| 2i |
| 1+i |
| 2i(1-i) |
| (1+i)(1-i) |
| 2i(1-i) |
| 2 |
∴
. |
| z |
则z=2-i．
故选：B．
点评：本题考查了复数代数形式的除法运算，考查了共轭复数的概念，是基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
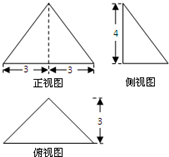如图是某个四面体的三视图，若在该四面体的外接球内任取一点，则点落在四面体内的概率为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f（x）的定义域为R，f（-1）=1，对任意x∈R，f′（x）＞3，则f（x）＞3x+4的解集为（ ）
| A、（-1，1） |
| B、（-1，+∞） |
| C、（-∞，-1） |
| D、（-∞，+∞） |
已知2x=3y=a，且
+
=2，则a的值为（ ）
| 1 |
| x |
| 1 |
| y |
A、
| ||
| B、6 | ||
C、±
| ||
| D、36 |
已知集合M={x∈Z|log3x≤1}，N={x∈Z|x2-2x＜0}，则（ ）
| A、M=N | B、M∩N=∅ |
| C、M∩N=R | D、M?N |