题目内容
对任意非负实数x,不等式(
-
)•
≤a恒成立,则实数a的最小值为 .
| x+1 |
| x |
| x |
考点:函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:令f(x)=(
-
)•
,讨论x=0和x>0时,运用分离变量法,求得函数f(x)的范围,再由恒成立思想即可得到a的范围和最小值.
| x+1 |
| x |
| x |
解答:
解:令f(x)=(
-
)•
,
则f(x)=
=
当x=0时,f(x)=0;
当x≠0时,f(x)=
∈(0,
),
不等式(
-
)•
≤a恒成立,
即有a≥
.
则实数a的最小值为
.
故答案为:
.
| x+1 |
| x |
| x |
则f(x)=
| ||||
|
| ||||
|
当x=0时,f(x)=0;
当x≠0时,f(x)=
| 1 | ||||
1+
|
| 1 |
| 2 |
不等式(
| x+1 |
| x |
| x |
即有a≥
| 1 |
| 2 |
则实数a的最小值为
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查不等式的恒成立问题转化为求函数的最值,运用函数的性质求出函数的范围是解题的关键.

练习册系列答案
相关题目
过点M(1,
)向抛物线C:y2=ax的准线作垂线,垂足为D,若|MD|=|MO|(其中O是坐标原点),则a=( )
| a |
| A、8 | B、4 | C、6 | D、-8或8 |
已知函数f(x)=
,若g(x)=|f(x)|-ax-a的图象与x轴有3个不同的交点,则实数a的取值范围是( )
|
A、(0,
| ||||
B、(0,
| ||||
C、[
| ||||
D、[
|
已知圆O:x2+y2=1和直线l:y=kx+
,则k=1是圆O与直线l相切的( )
| 2 |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
如图所示的程序框图的输出值y∈(1,2],则输入值x的范围是( )
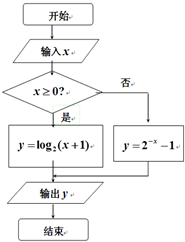

| A、(-∞,3] |
| B、[-1,log23) |
| C、[-log23,-1)∪(1,3] |
| D、[-log23,0)∪(1,3] |