题目内容
在数列{an}中,a1=3,an=
,bn=an-2,n=2,3,
(Ⅰ)求a2,a3,判断数列{an}的单调性并证明;
(Ⅱ)求证:|an-2|<
|an-1-2|(n=2,3,…);
(Ⅲ)是否存在常数M,对任意n≥2,有b2b3…bn≤M?若存在,求出M的值;若不存在,请说明理由.
| an-1+2 |
(Ⅰ)求a2,a3,判断数列{an}的单调性并证明;
(Ⅱ)求证:|an-2|<
| 1 |
| 4 |
(Ⅲ)是否存在常数M,对任意n≥2,有b2b3…bn≤M?若存在,求出M的值;若不存在,请说明理由.
考点:数列递推式,数列与不等式的综合
专题:点列、递归数列与数学归纳法,不等式的解法及应用
分析:(Ⅰ)由a1=3,an=
,得a2=
,a3=
,且可知an>0.再由an=
,两边平方得an2=an-1+2,进一步得到an+12=an+2,
两式作差可得an+1-an与an-an-1同号.由a2-a1=
-3<0易知,an-an-1<0,即an<an-1,可知数列{an}单调递减;
(Ⅱ)由an2=an-1+2,可得,an2-4=an-1-2,(an-2)(an+2)=an-1-2,进一步得到|an-2|=
.由an-2与an-1-2同号,可得an-2>0,即an>2,可得
<
,则|an-2|<
|an-1-2|;
(Ⅲ)由(an-2)(an+2)=an-1-2,得an+2=
,即bn=
,累积后由|an-2|<
|an-1-2|,可知|an-2|<
|an-1-2|<
|an-2-2|<
|an-3-2|<…<
|a1-2|=
,得
>4n-1,由an>2,得
>4n-1.结合当n→∞时,4n-1→∞,说明不存在常数M,对任意n≥2,有b2b3…bn≤M成立.
| an-1+2 |
| 5 |
|
| an-1+2 |
两式作差可得an+1-an与an-an-1同号.由a2-a1=
| 5 |
(Ⅱ)由an2=an-1+2,可得,an2-4=an-1-2,(an-2)(an+2)=an-1-2,进一步得到|an-2|=
| |an-1-2| |
| an+2 |
| 1 |
| an+2 |
| 1 |
| 4 |
| 1 |
| 4 |
(Ⅲ)由(an-2)(an+2)=an-1-2,得an+2=
| an-1-2 |
| an-2 |
| an-1-2 |
| an-2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 42 |
| 1 |
| 43 |
| 1 |
| 4n-1 |
| 1 |
| 4n-1 |
| 1 |
| |an-2| |
| 1 |
| an-2 |
解答:
(Ⅰ)解:由a1=3,an=
,得a2=
,a3=
,且可知an>0.
由an=
,得an2=an-1+2(1),
则有an+12=an+2(2),
由(2)-(1)得:an+12-an2=an-an-1,
(an+1+an)(an+1-an)=an-an-1,
∵an>0,∴an+1-an与an-an-1同号.由a2-a1=
-3<0,
易知,an-an-1<0,即an<an-1,可知数列{an}单调递减;
(Ⅱ)证明:由an2=an-1+2,可得,an2-4=an-1-2,(an-2)(an+2)=an-1-2,
∴|an-2|=
.
由(an-2)(an+2)=an-1-2,易知,an-2与an-1-2同号,
由于a1-2=3-2>0,可知,an-2>0,即an>2,
∴an+2>4,∴
<
,
∴|an-2|<
|an-1-2|,得证;
(Ⅲ)解:∵(an-2)(an+2)=an-1-2,
∴an+2=
,即bn=
,
则b2b3…bn=
•
…
=
=
.
由|an-2|<
|an-1-2|,可知,
|an-2|<
|an-1-2|<
|an-2-2|<
|an-3-2|<…<
|a1-2|=
,
∴
>4n-1,
∵an>2,
∴
>4n-1.
当n→∞时,4n-1→∞,
故不存在常数M,对任意n≥2,有b2b3…bn≤M成立.
| an-1+2 |
| 5 |
|
由an=
| an-1+2 |
则有an+12=an+2(2),
由(2)-(1)得:an+12-an2=an-an-1,
(an+1+an)(an+1-an)=an-an-1,
∵an>0,∴an+1-an与an-an-1同号.由a2-a1=
| 5 |
易知,an-an-1<0,即an<an-1,可知数列{an}单调递减;
(Ⅱ)证明:由an2=an-1+2,可得,an2-4=an-1-2,(an-2)(an+2)=an-1-2,
∴|an-2|=
| |an-1-2| |
| an+2 |
由(an-2)(an+2)=an-1-2,易知,an-2与an-1-2同号,
由于a1-2=3-2>0,可知,an-2>0,即an>2,
∴an+2>4,∴
| 1 |
| an+2 |
| 1 |
| 4 |
∴|an-2|<
| 1 |
| 4 |
(Ⅲ)解:∵(an-2)(an+2)=an-1-2,
∴an+2=
| an-1-2 |
| an-2 |
| an-1-2 |
| an-2 |
则b2b3…bn=
| a1-2 |
| a2-2 |
| a2-2 |
| a3-2 |
| an-1-2 |
| an-2 |
| a1-2 |
| an-2 |
| 1 |
| an-2 |
由|an-2|<
| 1 |
| 4 |
|an-2|<
| 1 |
| 4 |
| 1 |
| 42 |
| 1 |
| 43 |
| 1 |
| 4n-1 |
| 1 |
| 4n-1 |
∴
| 1 |
| |an-2| |
∵an>2,
∴
| 1 |
| an-2 |
当n→∞时,4n-1→∞,
故不存在常数M,对任意n≥2,有b2b3…bn≤M成立.
点评:本题是数列与不等式的综合题,考查了数列递推式,训练了累积法求数列的通项公式,训练了放缩法证明数列不等式,属难题.

练习册系列答案
 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
已知函数f(x)满足f(x)=f(
)且当x∈[
,1]时,f(x)=lnx,若当x∈[
,π]时,函数g(x)=f(x)-ax与x轴有交点,则实数a的取值范围是( )
| 1 |
| x |
| 1 |
| π |
| 1 |
| π |
A、[-
| ||||
| B、[-πlnπ,0] | ||||
C、[-
| ||||
D、[-
|
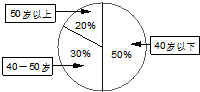 某单位200名职工的年龄分布情况如图示,该单位为了解职工每天的睡眠情况,按年龄用分层抽样方法从中抽取40名职工进行调查.则应从40-50岁的职工中抽取的人数为( )
某单位200名职工的年龄分布情况如图示,该单位为了解职工每天的睡眠情况,按年龄用分层抽样方法从中抽取40名职工进行调查.则应从40-50岁的职工中抽取的人数为( )