题目内容
已知函数f(x)=
,若g(x)=|f(x)|-ax-a的图象与x轴有3个不同的交点,则实数a的取值范围是( )
|
A、(0,
| ||||
B、(0,
| ||||
C、[
| ||||
D、[
|
考点:分段函数的应用,函数的图象
专题:数形结合,函数的性质及应用
分析:由题意可得|f(x)|=a(x+1)有3个不同的实根,即有函数y=|f(x)|与y=a(x+1)的图象有3个交点,作出函数y=|f(x)|与y=a(x+1)的图象,考虑直线经过点(2,ln3)和y=ln(x+1)(0<x≤2)相切的情况,求得a,运用导数的几何意义,即可得到a,进而通过图象观察即可得到所求范围.
解答:
 解:g(x)=|f(x)|-ax-a的图象与x轴有3个不同的交点,
解:g(x)=|f(x)|-ax-a的图象与x轴有3个不同的交点,
则|f(x)|=a(x+1)有3个不同的实根,
即有函数y=|f(x)|与y=a(x+1)的图象有3个交点,
作出函数y=|f(x)|与y=a(x+1)的图象,
当直线经过点(2,ln3)两图象有3个交点,即有a=
;
当直线与y=ln(x+1)(0<x≤2)相切时,两图象有2个交点.
设切点为(m,n),则切线的斜率为
=a,
又n=a(m+1),n=ln(m+1).
解得a=
,m=e-1<2,
则图象与x轴有3个不同的交点,即有a的取值范围是[
,
).
故选C.
 解:g(x)=|f(x)|-ax-a的图象与x轴有3个不同的交点,
解:g(x)=|f(x)|-ax-a的图象与x轴有3个不同的交点,则|f(x)|=a(x+1)有3个不同的实根,
即有函数y=|f(x)|与y=a(x+1)的图象有3个交点,
作出函数y=|f(x)|与y=a(x+1)的图象,
当直线经过点(2,ln3)两图象有3个交点,即有a=
| ln3 |
| 3 |
当直线与y=ln(x+1)(0<x≤2)相切时,两图象有2个交点.
设切点为(m,n),则切线的斜率为
| 1 |
| 1+m |
又n=a(m+1),n=ln(m+1).
解得a=
| 1 |
| e |
则图象与x轴有3个不同的交点,即有a的取值范围是[
| ln3 |
| 3 |
| 1 |
| e |
故选C.
点评:本题考查分段函数的运用,主要考查分段函数的图象,以及函数方程的转化,运用数形结合的思想方法是解题的关键.

练习册系列答案
相关题目
已知集合A={3,4},集合B={1,2,3,4},则∁BA=( )
| A、∅ |
| B、{3,4} |
| C、{1,2} |
| D、{1,2,3,4,5} |
若等边△ABC的边长为2
,平面内一点M满足:
=
+
,则
•
=( )
| 3 |
| CM |
| 1 |
| 6 |
| CB |
| 2 |
| 3 |
| CA |
| MA |
| MB |
| A、-1 | B、2 | C、-2 | D、3 |
定义域为R的函数f(x)满足f(x+2)=2f(x)-2,当x∈(0,2]时,f(x)=
,若x∈(0,4]时,t2-
≤f(x)恒成立,则实数t的取值范围是( )
|
| 7t |
| 2 |
| A、[1,2] | ||
B、[2,
| ||
C、[1,
| ||
| D、[2,+∞) |
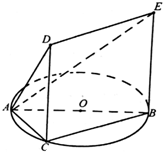 如图,已知五面体ABCDE,其中△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.
如图,已知五面体ABCDE,其中△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.