题目内容
过点M（1，
）向抛物线C：y2=ax的准线作垂线，垂足为D，若|MD|=|MO|（其中O是坐标原点），则a=（ ）
| a |
| A、8 | B、4 | C、6 | D、-8或8 |
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：求出抛物线的准线方程，利用距离公式列出方程，即可求出a的值．
解答：
解：抛物线C：y2=ax的准线为x=-
．
过点M（1，
）向抛物线C：y2=ax的准线作垂线，垂足为D，若|MD|=|MO|，
可得：1+
=
，
即16+16a=（4+a）2，
解得a=8．a=0（舍去）．
故选：A．
| a |
| 4 |
过点M（1，
| a |
可得：1+
| a |
| 4 |
1+(
|
即16+16a=（4+a）2，
解得a=8．a=0（舍去）．
故选：A．
点评：本题考查抛物线的性质，两点间距离公式的应用，考查计算能力．
练习册系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
已知集合A={3，4}，集合B={1，2，3，4}，则∁BA=（ ）
| A、∅ |
| B、{3，4} |
| C、{1，2} |
| D、{1，2，3，4，5} |
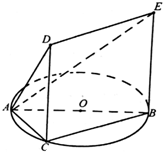如图，已知五面体ABCDE，其中△ABC内接于圆O，AB是圆O的直径，四边形DCBE为平行四边形，且DC⊥平面ABC．