题目内容
关于x的方程x2•log
a-(2x+1)=0有实数根,则a的取值范围是 .
| 1 |
| 2 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:若关于x的方程x2•log
a-(2x+1)=0有实数根,则△=4+4log
a≥0,解对数不等式可得a的取值范围.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:若关于x的方程x2•log
a-(2x+1)=0有实数根,
则△=4+4log
a≥0,
即log
a≥-1,
故0<a≤2,
故a的取值范围是(0,2],
故答案为:(0,2]
| 1 |
| 2 |
则△=4+4log
| 1 |
| 2 |
即log
| 1 |
| 2 |
故0<a≤2,
故a的取值范围是(0,2],
故答案为:(0,2]
点评:本题考查的知识点是根的存在性及根的个数判断,其中根据一元二次方程根的个数与△的关系,构造关于a的不等式是解答的关键.

练习册系列答案
相关题目
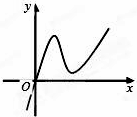 定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示,若两正数a、b满足f(2a+b)<1,则
定义在R上的函数f(x)满足f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示,若两正数a、b满足f(2a+b)<1,则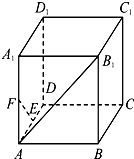
 如图是一个平面图形的直观图,在直观图中,O′C′=O′D′=2,O′A′=3,则原平面图形的面积为
如图是一个平面图形的直观图,在直观图中,O′C′=O′D′=2,O′A′=3,则原平面图形的面积为