题目内容
设点A(-2,3),B(3,1),若直线ax+y+2=0与线段AB没有交点,则a的取值范围是( )
A、(-∞,-
| ||
B、(-1,
| ||
C、[-
| ||
D、(-∞,-1]∪[
|
考点:直线的斜率
专题:直线与圆
分析:直线ax+y+2=0过P(0,-2),斜率为-a,由已知条件推导出kPA<-a<kPB,由此能求出a的取值范围.
解答:
解:如图,直线ax+y+2=0过P(0,-2),斜率为-a,
∵点A(-2,3),B(3,1),
直线ax+y+2=0与线段AB没有交点,
∴kPA<-a<kPB,
∴
<-a<
,即-
<-a<1,
∴-1<a<
,
∴a的取值范围是(-1,
).
故选:B.

∵点A(-2,3),B(3,1),
直线ax+y+2=0与线段AB没有交点,
∴kPA<-a<kPB,
∴
| 3+2 |
| -2-0 |
| 1+2 |
| 3-0 |
| 5 |
| 2 |
∴-1<a<
| 5 |
| 2 |
∴a的取值范围是(-1,
| 5 |
| 2 |
故选:B.
点评:本题考查实数的取值范围的求法,是中档题,解题时要认真审题,注意数形结合思想的合理运用.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
已知|
|=1,|
|=
,且向量(
-
)和
垂直,则
•
的值为( )
| a |
| b |
| 2 |
| a |
| b |
| a |
| a |
| b |
| A、0 | ||
| B、1 | ||
C、
| ||
D、-
|
执行如图所示的程序框图,则输出结果为( )


| A、初始输入中的a值 |
| B、三个数中的最大值 |
| C、三个数中的最小值 |
| D、初始输入中的c值 |
等比数列{an}中,a5=-2,则此数列前9项的积为( )
| A、256 | B、-256 |
| C、-512 | D、512 |
在等比数列{an}中,已知a1=1,a4=8,则a6=( )
| A、16 | B、16或-16 |
| C、32 | D、32或-32 |
已知函数f(x)=-2cosx,x∈[0,π]在点P处的切线与函数g(x)=
x2+lnx在点Q处的切线平行,则直线PQ的斜率为( )
| 1 |
| 2 |
A、
| ||
B、
| ||
| C、2 | ||
| D、π-2 |
已知向量
=(-1,2),
=(10,5),则
与
( )
| a |
| b |
| a |
| b |
| A、垂直 | B、平行 |
| C、相交但不垂直 | D、无法判断 |
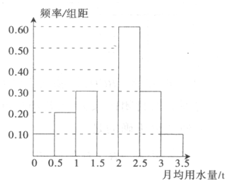 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准?用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图,
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准?用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图,