题目内容
国家标准规定:轻型汽车的氮氧化物排放量不得超过80mg/km.根据这个标准,检测单位从某出租车公司运营的A、B两种型号的出租车中分别抽取6辆,对其氮氧化物的排放量进行检测,检测结果记录如下:(单位:mg/km)
由于表格被污损,数据x看不清,统计员只记得A、B两种出租车的氮氧化物排放量的平均值相等,且方差分别记为sA2,sB2.
(1)求x及sB2的值;
(2)从被检测的6辆B种型号的出租车中任取3辆,记“氮氧化物排放量未超过80mg/km”的车辆数为ξ,求ξ的分布列和数学期望.
| A | 85 | 80 | 85 | 60 | 90 |
| B | 70 | x | 95 | y | 75 |
(1)求x及sB2的值;
(2)从被检测的6辆B种型号的出租车中任取3辆,记“氮氧化物排放量未超过80mg/km”的车辆数为ξ,求ξ的分布列和数学期望.
考点:离散型随机变量的期望与方差,众数、中位数、平均数,极差、方差与标准差
专题:应用题,概率与统计
分析:(1)利用A、B两种出租车的氮氧化物排放量的平均值相等,计算x,从而可求sB2的值;
(2)随机变量ξ=0,1,2,然后利用古典概型的概率公式求出相应的概率,列出分布列,最后利用数学期望的公式解之即可.
(2)随机变量ξ=0,1,2,然后利用古典概型的概率公式求出相应的概率,列出分布列,最后利用数学期望的公式解之即可.
解答:
解:(1)由条件知85+80+85+60+90+80=70+80+95+x+75+70
∴x=90,
∴
=
[(70-80)2+(80-80)2+(95-80)2+(90-80)2+(75-80)2+(70-80)2]=
(2)由条件知ξ=0,1,2,3,
P(ξ=0)=
=
,P(ξ=1)=
=
,P(ξ=2)=
=
,P(ξ=3)=
=
.
ξ的分布列为:
故E(ξ)=0×
+1×
+2×
+3×
=
∴x=90,
∴
| S | 2 B |
| 1 |
| 6 |
| 350 |
| 3 |
(2)由条件知ξ=0,1,2,3,
P(ξ=0)=
| ||||
|
| 1 |
| 20 |
| ||||
|
| 9 |
| 20 |
| ||||
|
| 9 |
| 20 |
| ||||
|
| 1 |
| 20 |
ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 1 |
| 20 |
| 9 |
| 20 |
| 9 |
| 20 |
| 1 |
| 20 |
| 3 |
| 2 |
点评:本题主要考查了平均数、方差、分布列,以及离散型随机变量的期望,同时考查了运算求解的能力,属于中档题.

练习册系列答案
相关题目
等比数列{an}中,a5=-2,则此数列前9项的积为( )
| A、256 | B、-256 |
| C、-512 | D、512 |
下列框图属于流程图的是( )
A、 |
B、 |
C、 |
D、 |
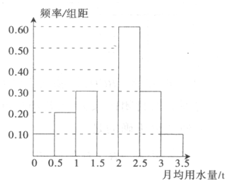 我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准?用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图,
我国是世界上严重缺水的国家之一,城市缺水问题较为突出.某市为了节约生活用水,计划在本市试行居民生活用水定额管理(即确定一个居民月均用水量标准?用水量不超过a的部分按照平价收费,超过a的部分按照议价收费).为了较为合理地确定出这个标准,通过抽样获得了 100位居民某年的月均用水量(单位:t),制作了频率分布直方图,