Question

在△AOB中，∠AOB=

3

4

π，点O到直线AB的距离为10，则边AB的最小值为．

 

．

Answer 1

考点：解三角形

专题：解三角形

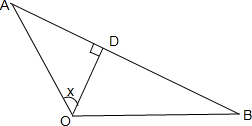
分析：作OD⊥AB于D，假设∠AOD=x，则∠BOD=

3π

4

-x，可求得AB=10[（tanx-1）+

2

tanx-1

+2]，利用基本不等式即可求得答案．

解答： 解：作OD⊥AB于D，假设∠AOD=x，则∠BOD=

3π

4

-x，因为OD=10，

所以AB=AD+BD=10tgx+10tg（

3π

4

-x）=10[tgx-tg（x+

π

4

）]
=10tan[x-（x+

π

4

）][1+tanxtan（x+

π

4

）]
=-10（1+tanx•

1+tanx

1-tanx

）
=-10×

1-tanx+tanx+tan2x

1-tanx

=-10×

(1-tanx)2+2tanx

1-tanx

=-10[（1-tanx）+

2

1-tanx

-2]
=10[（tanx-1）+

2

tanx-1

+2]，依题意，x＞

π

4

，tanx＞1，
所以，上式≥10×（2

2

+2）=20

2

+20，当且仅当tanx-1=

2

tanx-1

，
即tanx=

2

+1，x=arctan（

2

+1）时取“=”．
故边AB的最小值为20

2

+20，
故答案为：20

2

+20．

点评：本题考查解三角形，考查两角差的正切的应用，求得AB=10[（tanx-1）+

2

tanx-1

+2]是关键，突出考查转化思想与基本不等式的应用，属于难题．