题目内容
对于空间的两条直线m、n和一个平面α,下列命题中的真命题是( )
| A、若m∥α,n∥α,则m∥n |
| B、若m∥α,n?α,则m∥n |
| C、若m∥α,n⊥α,则m∥n |
| D、若m⊥α,n⊥α,则m∥n |
考点:命题的真假判断与应用,空间中直线与直线之间的位置关系,空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:A.利用线面平行的性质定理即可得出;
B.利用线面平行的性质定理即可得出;
C.利用线面平行与垂直的性质定理即可得出;
D.利用线面垂直的性质定理即可得出.
B.利用线面平行的性质定理即可得出;
C.利用线面平行与垂直的性质定理即可得出;
D.利用线面垂直的性质定理即可得出.
解答:
解:A.若m∥α,n∥α,则m∥n、相交或为异面直线,因此A不正确;
B.若m∥α,n?α,则m∥n或为异面直线,因此B不正确;
C.若m∥α,n⊥α,则m⊥n,因此C不正确;
D.若m⊥α,n⊥α,利用线面垂直的性质定理可知:m∥n.正确.
故选:D.
B.若m∥α,n?α,则m∥n或为异面直线,因此B不正确;
C.若m∥α,n⊥α,则m⊥n,因此C不正确;
D.若m⊥α,n⊥α,利用线面垂直的性质定理可知:m∥n.正确.
故选:D.
点评:本题综合考查了线面平行与垂直的性质定理,属于基础题.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
已知函数f(x)是奇函数,且x∈(0,2)时,f(x)=2x,则f(-1)=( )
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|
 如图,在正方体AC1中,E、F分别是AB和AA1的中点,则下列命题:
如图,在正方体AC1中,E、F分别是AB和AA1的中点,则下列命题:①E、C、D1、F四点共面;
②CE、D1F、DA三线共点;
③EF和BD1所成的角为45°;
④A1B∥平面CD1E;
⑤B1D⊥平面CD1E.
其中,正确的个数是( )
| A、2 个 | B、3个 |
| C、4个 | D、5个 |
给出下列四个命题:
①?x∈R,x2+2>0
②?x∈N,x4≥1
③?x0∈Z,x03<1
④?x0∈Q,x02=3
其中是真命题是( )
①?x∈R,x2+2>0
②?x∈N,x4≥1
③?x0∈Z,x03<1
④?x0∈Q,x02=3
其中是真命题是( )
| A、①② | B、④① | C、③④ | D、③① |
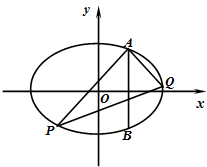 如图,两条相交线段AB、PQ的四个端点都在椭圆
如图,两条相交线段AB、PQ的四个端点都在椭圆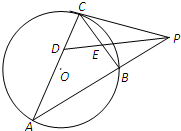 如图,PC是圆O的切线,切点为C,直线PA与圆O交于A、B两点,∠APC的平分线分别交弦CA,CB于D,E两点,已知PC=3,PB=2,则
如图,PC是圆O的切线,切点为C,直线PA与圆O交于A、B两点,∠APC的平分线分别交弦CA,CB于D,E两点,已知PC=3,PB=2,则