题目内容
已知f(x)=2sinxcosx+2cos2x
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)当x∈[0,
]时,求函数f(x)的最大值及取得最大值的x值.
(Ⅰ)求函数f(x)的最小正周期;
(Ⅱ)当x∈[0,
| π |
| 2 |
考点:两角和与差的正弦函数,三角函数的周期性及其求法,三角函数的最值
专题:计算题,三角函数的图像与性质
分析:(Ⅰ)由倍角公式化简可得函数解析式为f(x)=
sin(2x+
)+1,由三角函数的周期性及其求法即可求解.
(Ⅱ)由已知可得2x+
∈[
,
],根据正弦函数的图象和性质即可求得函数f(x)的最大值及取得最大值的x值.
| 2 |
| π |
| 4 |
(Ⅱ)由已知可得2x+
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
解答:
解:(Ⅰ)∵f(x)=2sinxcosx+2cos2x=sin2x+cos2x+1=
sin(2x+
)+1,
∴T=
=π.
(Ⅱ)∵x∈[0,
],
∴2x+
∈[
,
],
∴当2x+
=
即有x=
时,f(x)max=
+1,
当2x+
=
即有x=
时,f(x)min=1-
.
| 2 |
| π |
| 4 |
∴T=
| 2π |
| 2 |
(Ⅱ)∵x∈[0,
| π |
| 2 |
∴2x+
| π |
| 4 |
| π |
| 4 |
| 5π |
| 4 |
∴当2x+
| π |
| 4 |
| π |
| 2 |
| π |
| 8 |
| 2 |
当2x+
| π |
| 4 |
| 5π |
| 4 |
| π |
| 2 |
| 2 |
点评:本题主要考查了三角函数的周期性及其求法,两角和与差的正弦函数公式的应用,三角函数的最值,属于基础题.

练习册系列答案
相关题目
圆x2+y2-2x+4y-4=0截直线 x+y-l=0所截得的弦长是( )
| A、2 | ||
B、2
| ||
C、2
| ||
| D、以上都不对 |
一个不透明的袋中装有除颜色外其余均相同的4个红球和9个白球,从中随即摸出一个,则摸到白球的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知命题p:“?x∈[1,2],2x2-a≥0”,命题q:“?x∈R,x2+2ax+2-a=0”,若命题“p且q”是真命题,则实数a的取值范围是( )
| A、a≤-2或1≤a≤2 |
| B、a<-2或1<a≤2) |
| C、a≤-2或1≤a<2 |
| D、a<-2或1<a<2 |
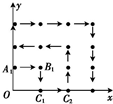 为防洪抗旱,某地区大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在A1(0,1)点,第二棵树在B1(1,1)点,第三棵树在C1(1,0)点,第四棵树在C2(2,0)点,接着按图中箭头方向每隔一个单位长度种一棵树,那么,第2013棵树所在的点的坐标是
为防洪抗旱,某地区大面积植树造林,如图,在区域{(x,y)|x≥0,y≥0}内植树,第一棵树在A1(0,1)点,第二棵树在B1(1,1)点,第三棵树在C1(1,0)点,第四棵树在C2(2,0)点,接着按图中箭头方向每隔一个单位长度种一棵树,那么,第2013棵树所在的点的坐标是