题目内容
在△ABC中，角A，B，C所对分别为a，b，c，且1+
=
．
（I）求角A：
（II）若向量
=（0，-1），
=（cosB，2cos2
），
试求|m+n|的最小值．
| tanA |
| tanB |
| 2c |
| b |
（I）求角A：
（II）若向量
| m |
| n |
| C |
| 2 |
试求|m+n|的最小值．
考点：正弦定理的应用,平面向量数量积的运算
专题：计算题,三角函数的求值,三角函数的图像与性质,解三角形,平面向量及应用
分析：（Ⅰ）运用正弦定理，将边化为角，由同角的商数关系和两角和的正弦公式，化简计算即可得到A；
（Ⅱ）由向量的加法运算和向量的模的公式，结合两角差的余弦公式和正弦公式，再由正弦函数的图象和性质，即可求得最小值．
（Ⅱ）由向量的加法运算和向量的模的公式，结合两角差的余弦公式和正弦公式，再由正弦函数的图象和性质，即可求得最小值．
解答：
解：（I）由正弦定理，1+
=
即为
1+
=
，即
=
则cosA=
，0＜A＜π，
则A=
；
（II）向量
=（0，-1），
=（cosB，2cos2
），
|
+
|=|（cosB，2cos2
-1）|=|（cosB，cosC）|
=
=
=
=
，
因为A=
，所以B∈（0，
），2B-
∈（-
，
），
sin（2B-
）∈（-
，1]，
当sin（2B-
）=1即B=
时，
|
+
|取得最小值，且为
．
| tanA |
| tanB |
| 2c |
| b |
1+
| ||
|
| 2sinC |
| sinB |
| sinAcosB+cosAsinB |
| sinBcosA |
| 2sin(A+B) |
| sinB |
则cosA=
| 1 |
| 2 |
则A=
| π |
| 3 |
（II）向量
| m |
| n |
| C |
| 2 |
|
| m |
| n |
| C |
| 2 |
=
| cos2B+cos2C |
=
cos2B+cos2(
|
=
1+
|
1-
|
因为A=
| π |
| 3 |
| 2π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
sin（2B-
| π |
| 6 |
| 1 |
| 2 |
当sin（2B-
| π |
| 6 |
| π |
| 3 |
|
| m |
| n |
| ||
| 2 |
点评：本题考查正弦定理和三角函数的化简和求值，考查向量和的模的大小的求法，解题时要认真审题，注意三角函数公式的合理运用．
练习册系列答案
相关题目
下列函数为奇函数的是（ ）
| A、y=x2-1 | ||
| B、y=2x | ||
C、y=
| ||
D、y=
|
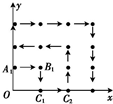为防洪抗旱，某地区大面积植树造林，如图，在区域{（x，y）|x≥0，y≥0}内植树，第一棵树在A1（0，1）点，第二棵树在B1（1，1）点，第三棵树在C1（1，0）点，第四棵树在C2（2，0）点，接着按图中箭头方向每隔一个单位长度种一棵树，那么，第2013棵树所在的点的坐标是