题目内容
已知变量x，y满足
，则z=log2x+log2y+1的最大值为 ．
|
考点：简单线性规划
专题：综合题,不等式的解法及应用
分析：由题意，z=log2x+log2y+1=log2xy+1，问题转化为求xy的最大值，再由变量x，y满足
，作出其对应的区域，判断出最值即可．
|
解答：
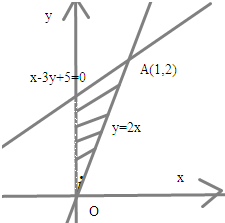解：由于z=log2x+log2y+1=log2xy+1，问题转化为求xy的最大值，
变量x，y满足
，其对应的区域如图，
由图知，当x=1，y=2时，xy的最大值为2，
故z=log2x+log2y+1=log2xy+1，的最大值为2
故答案为：2．
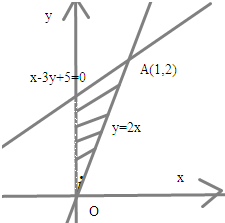解：由于z=log2x+log2y+1=log2xy+1，问题转化为求xy的最大值，变量x，y满足
|
由图知，当x=1，y=2时，xy的最大值为2，
故z=log2x+log2y+1=log2xy+1，的最大值为2
故答案为：2．
点评：本题考查简单线性规划的应用，数形结合是本题的解答特点，本题考查了转化的思想，对数函数的单调性，涉及到的知识点较多．
练习册系列答案
相关题目
若f（x）是定义在（0，+∞）上的增函数，且f（
）=f（x）-f（y）．
（1）求f（1）的值；
（2）解不等式：f（x-1）＜0；
（3）若f（2）=1，解不等式f（2x+1）-f（23-2x）＜2．
| x |
| y |
（1）求f（1）的值；
（2）解不等式：f（x-1）＜0；
（3）若f（2）=1，解不等式f（2x+1）-f（23-2x）＜2．
已知|
|=1，|
|=
，且
•（2
+
）=1，则
与
夹角的余弦值为（ ）
| a |
| b |
| 2 |
| b |
| a |
| b |
| a |
| b |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|