题目内容
已知数列{an}的前6项如下表所示,其中奇数项成等差数列,偶数项成等比数列.
(1)写出数列{an}的通项公式(不要求推理过程);
(2)当n是偶数时,求Sn=a1a2+a3a4+a5a6+…+an-1an;
(3)当n是奇数时,求数列{an}的前n项和Tn.
| n | 1 | 2 | 3 | 4 | 5 | 6 | … |
| an | 1 | 2 | 3 | 4 | 5 | 8 | … |
(2)当n是偶数时,求Sn=a1a2+a3a4+a5a6+…+an-1an;
(3)当n是奇数时,求数列{an}的前n项和Tn.
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由题意,当n是奇数时,显然有an=n;当n是偶数时,有an=2
;即可得出.
(2)利用“错位相减法”即可得出.
(3)当n是奇数时,Tn=(a1+a3+…+an)+(a2+a4+…+an-1),分别利用等差数列与等比数列的前n项和公式即可得出.
| n |
| 2 |
(2)利用“错位相减法”即可得出.
(3)当n是奇数时,Tn=(a1+a3+…+an)+(a2+a4+…+an-1),分别利用等差数列与等比数列的前n项和公式即可得出.
解答:
解:(1)由题意,当n是奇数时,显然有an=n;
当n是偶数时,有an=2
;
故通项an=
.
(2)当n是偶数时,Sn=a1a2+a3a4+a5a6+…+an-1an
=1×2+3×22+…+(n-1)×2
,
则2Sn=1×22+3×23+…+(n-1)×2
+1,
两式相减可得:-Sn=1×2+2×(22+23+…+2
)-(n-1)×2
+1
=2+2×
-(n-1)×2
+1
=-(n-3)×2
+1-6,
∴Sn=(n-3)×2
+1+6.
(3)当n是奇数时,Tn=(a1+a3+…+an)+(a2+a4+…+an-1)
=(1+3+5+…+n)+(2+22+23+…+2
)
=
×
+
=(
)2+2
-2.
当n是偶数时,有an=2
| n |
| 2 |
故通项an=
|
(2)当n是偶数时,Sn=a1a2+a3a4+a5a6+…+an-1an
=1×2+3×22+…+(n-1)×2
| n |
| 2 |
则2Sn=1×22+3×23+…+(n-1)×2
| n |
| 2 |
两式相减可得:-Sn=1×2+2×(22+23+…+2
| n |
| 2 |
| n |
| 2 |
=2+2×
4(2
| ||
| 2-1 |
| n |
| 2 |
=-(n-3)×2
| n |
| 2 |
∴Sn=(n-3)×2
| n |
| 2 |
(3)当n是奇数时,Tn=(a1+a3+…+an)+(a2+a4+…+an-1)
=(1+3+5+…+n)+(2+22+23+…+2
| n-1 |
| 2 |
=
| n+1 |
| 2 |
| 1+n |
| 2 |
2(1-2
| ||
| 1-2 |
=(
| n+1 |
| 2 |
| n+1 |
| 2 |
点评:本题考查了“错位相减法”、等差数列与等比数列的通项公式及前n项和公式,考查了分类讨论的思想方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
把球的大圆面积扩大为原来的2倍,那么体积扩大为原来的( )
| A、2倍 | ||
B、2
| ||
C、
| ||
D、3
|
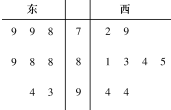 某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.