题目内容
证明：若a2-4b2-2a+1≠0，则a≠2b+1．
考点：反证法与放缩法
专题：证明题,推理和证明
分析：原命题不好证明，利用反证法进行证明即可，注意解题步骤．
解答：
证明：若a=2b+1，即a-2b=1，
则a2-4b2-2a+1=（a+2b）（a-2b）+1-2a
=a+2b+1-2a=1-（a-2b）=1-1=0，
这与条件a2-4b2-2a+1≠0矛盾，
则假设不成立，
故若a2-4b2-2a+1≠0，则a≠2b+1成立．
则a2-4b2-2a+1=（a+2b）（a-2b）+1-2a
=a+2b+1-2a=1-（a-2b）=1-1=0，
这与条件a2-4b2-2a+1≠0矛盾，
则假设不成立，
故若a2-4b2-2a+1≠0，则a≠2b+1成立．
点评：本题主要考查命题的证明，对于一些否定的命题和至多、至少的命题的证明，运用反证法证明是常用方法．
练习册系列答案
七彩题卡口算应用一点通系列答案
相关题目
已知集合A={x|-1＜x＜3}，B={x|log2x＜2}，则A∩B=（ ）
| A、（-1，3） |
| B、（0，4） |
| C、（0，3） |
| D、（-1，4） |
函数f（x）=
+
，x∈（0，
]的最小值是（ ）
| sinx |
| 2 |
| 2 |
| sinx |
| π |
| 2 |
| A、2 | ||
| B、1 | ||
C、
| ||
| D、不存在 |
过双曲线2x2-y2-2=0的右焦点作直线l交曲线于A、B两点，若|AB|=4则这样的直线存在（ ）
| A、0条 | B、1条 | C、2条 | D、3条 |
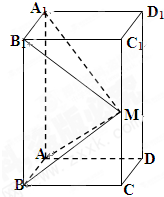如图，在长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，M为CC1的中点