题目内容
已知函数f(x)=
(其中e为自然对数的底)在区间(0,2)上有两个极值点x1,x2,且x1<x2,记实数m的取值范围为区间I.
(Ⅰ)求区间I;
(Ⅱ)记g(m)=x1+x2,证明:函数y=g(m)在区间I上单调递减.
| mex-2x-x2lnx |
| x2 |
(Ⅰ)求区间I;
(Ⅱ)记g(m)=x1+x2,证明:函数y=g(m)在区间I上单调递减.
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)根据极值的意义,利用导数判断函数的单调性,求函数的最值,即可得出结论;
(Ⅱ)利用(Ⅰ)的结论,结合函数单调性的定义加以证明.
(Ⅱ)利用(Ⅰ)的结论,结合函数单调性的定义加以证明.
解答:
解:(Ⅰ)f′(x)=
,
∵x∈(0,2),∴x-2<0,x3>0,
∴x1,x2是方程mex-x=0的两个不同的根,
即方程h(x)=
,h′(x)=
,
∴h(x)在(0,1]上递增,在[1,2]上递减,
又h(0)=0,h(1)=
,h(2)=
,
∴I∈(
,
).
(Ⅱ)设m1,m2∈I,且m1<m2,m1,m2对应的极值点分别是x1,x2和
,
,
∵h(x)=
在区间(0,1]上递增,在[1,2]上递减,
∴0<x1<
<1<
<x2,∴
>
>1,
又m1ex1=x1,m1ex2=x2,∴ex2-x1=
,
记
=t1,则x2-x1=lnt1,则x1=
,x2=
,g(m1)=
,
记
=t2,同理可得g(m2)=
,
记φ(t)=
,则φ′(t)=
,
令r(t)=-2lnt+t-
,则r′(t)=-
+1+
=(
-1)2,∴t≥1时,r′(t)≥0,
∴t>1时,r(t)>r(1)=0,∴φ′(t)>0,即φ(t)在区间(1,+∞)上单调递增,
∵t1>t2>1,∴φ(t1)>φ(t2),即g(m1)>g(m2),
∴函数y=g(m)在区间I上单调递减.
| (x-2)(mex-x) |
| x3 |
∵x∈(0,2),∴x-2<0,x3>0,
∴x1,x2是方程mex-x=0的两个不同的根,
即方程h(x)=
| x |
| ex |
| 1-x |
| ex |
∴h(x)在(0,1]上递增,在[1,2]上递减,
又h(0)=0,h(1)=
| 1 |
| e |
| 2 |
| e2 |
∴I∈(
| 2 |
| e2 |
| 1 |
| e |
(Ⅱ)设m1,m2∈I,且m1<m2,m1,m2对应的极值点分别是x1,x2和
| x | ′ 1 |
| x | ′ 2 |
∵h(x)=
| x |
| ex |
∴0<x1<
| x | ′ 1 |
| x | ′ 2 |
| x2 |
| x1 |
| ||
|
又m1ex1=x1,m1ex2=x2,∴ex2-x1=
| x2 |
| x1 |
记
| x2 |
| x1 |
| lnt1 |
| t1-1 |
| t1lnt1 |
| t1-1 |
| (t1+1)lnt1 |
| t1-1 |
记
| ||
|
| (t2+1)lnt2 |
| t2-1 |
记φ(t)=
| (t+1)lnt |
| t-1 |
-2lnt+t-
| ||
| (t-1)2 |
令r(t)=-2lnt+t-
| 1 |
| t |
| 2 |
| t |
| 1 |
| t2 |
| 1 |
| t |
∴t>1时,r(t)>r(1)=0,∴φ′(t)>0,即φ(t)在区间(1,+∞)上单调递增,
∵t1>t2>1,∴φ(t1)>φ(t2),即g(m1)>g(m2),
∴函数y=g(m)在区间I上单调递减.
点评:本题主要考查利用导数研究函数的单调性、极值、最值等知识,考查学生分析问题,解决问题的能力及运算求解能力,逻辑性、综合性强,属于难题.

练习册系列答案
相关题目
在△ABC中,A=60°,b=1,S△ABC=
,则
=( )
| 3 |
| a+b+c |
| sinA+sinB+sinC |
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
已知a,b是实数,则“|a-b|=|a|-|b|”是“ab>0”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
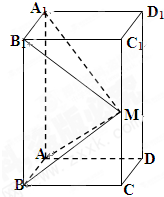 如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为CC1的中点
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,M为CC1的中点