题目内容
已知函数f(x)=
,若a、b、c互不相等,且f(a)=f(b)=f(c),则a+b+c取值范围为 .
|
考点:分段函数的应用
专题:计算题,函数的性质及应用
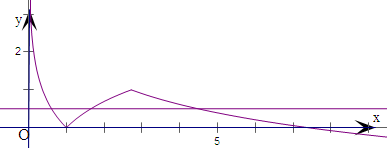
分析:画出函数的图象,判断a,b,c的范围,然后推出a+b+c的取值范围.
解答:
 解:函数f(x)=
解:函数f(x)=
,
若a,b,c互不相等,
且f(a)=f(b)=f(c),
如图,不妨设a<b<c,
由已知条件可知:
0<a<1<b<e<c<e2,
∵-lna=lnb,∴ab=1
∵lnb=2-1nc∴bc=e2,
∴a+b+c=b+
,(1<b<e),
由(b+
)′=1-
<0,故(1,e)为减区间,
∴2e+
<a+b+c<e2+2,
∴a+b+c的取值范围是:(2e+
,e2+2).
故答案为:(2e+
,e2+2).
 解:函数f(x)=
解:函数f(x)=
|
若a,b,c互不相等,
且f(a)=f(b)=f(c),
如图,不妨设a<b<c,
由已知条件可知:
0<a<1<b<e<c<e2,
∵-lna=lnb,∴ab=1
∵lnb=2-1nc∴bc=e2,
∴a+b+c=b+
| e2+1 |
| b |
由(b+
| e2+1 |
| b |
| e2+1 |
| b2 |
∴2e+
| 1 |
| e |
∴a+b+c的取值范围是:(2e+
| 1 |
| e |
故答案为:(2e+
| 1 |
| e |
点评:本题考查分段函数的应用,函数的零点的判定,考查数形结合的思想方法的应用,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
“m=1”是“直线x-my=1和直线x+my=0互相垂直”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知O为坐标原点,A(1,2),点P(x,y)满足约束条件
,则Z=
•
的最大值为( )
|
| OA |
| OP |
| A、-2 | B、-1 | C、1 | D、2 |
 如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,
如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,