题目内容
已知函数f(x)=lnx+
+b在点(1,3)处与y轴垂直.
(Ⅰ)求a,b的值;
(Ⅱ)求函数f(x)在[
,2]上的最大值和最小值.
| a |
| x |
(Ⅰ)求a,b的值;
(Ⅱ)求函数f(x)在[
| 1 |
| 2 |
考点:利用导数研究函数的极值,导数在最大值、最小值问题中的应用
专题:计算题,导数的综合应用
分析:(Ⅰ)求出函数的导数,由条件可得f′(1)=0且f(1)=3,即可得到a,b的值;
(Ⅱ)求出函数f(x)的导数,求出极值点,列表分析函数在[
,2]上的单调区间和极值,从而得到最小值和最大值.
(Ⅱ)求出函数f(x)的导数,求出极值点,列表分析函数在[
| 1 |
| 2 |
解答:
解:(Ⅰ)由于f(x)=lnx+
+b,
则f′(x)=
-
,
则
⇒
,
解得
;
(Ⅱ)由于f(x)=lnx+
+2,
则f′(x)=
-
=
由f'(x)=0⇒x=1,
列表如下
当x=1时,f(x)取得极小值即最小值:f(x)min=f(1)=3,
由于f(
)-f(2)=
-2ln2=lne
-ln4=ln
>0,
当x=
时,f(x)取得最大值f(x)max=f(
)=4-ln2.
| a |
| x |
则f′(x)=
| 1 |
| x |
| a |
| x2 |
则
|
|
解得
|
(Ⅱ)由于f(x)=lnx+
| 1 |
| x |
则f′(x)=
| 1 |
| x |
| 1 |
| x2 |
| x-1 |
| x2 |
由f'(x)=0⇒x=1,
列表如下
| x |
| (
| 1 | (1,2) | 2 | ||||
| y' | - | 0 | + | ||||||
| y | 4-ln2 | 单调递减 | 极小值 | 单调递增 |
|
由于f(
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
e
| ||
| 4 |
当x=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查导数的综合应用:求切线方程和求单调区间、极值和最值,考查运算能力,属于中档题.

练习册系列答案
相关题目
函数f(x)=(x-3)ex的单调递减区间是( )
| A、(-∞,2) |
| B、(0,3) |
| C、(1,4) |
| D、(2,+∞) |
已知O为坐标原点,A(1,2),点P(x,y)满足约束条件
,则Z=
•
的最大值为( )
|
| OA |
| OP |
| A、-2 | B、-1 | C、1 | D、2 |
 如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,
如图,在三棱柱ABC-A1B1C1中,△ABC是边长为2的等边三角形,AA1⊥平面ABC,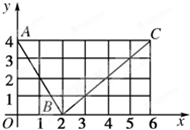 如图所示折线段ABC,其中A、B、C的坐标分别为(0,4),(2,0),(6,4).
如图所示折线段ABC,其中A、B、C的坐标分别为(0,4),(2,0),(6,4).