题目内容
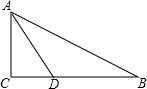如图，Rt△ABC中，∠C是直角，AD是∠BAC的平分线，已知AD=5，AC=4，求sin∠BAC的值．考点：解三角形的实际应用
专题：解三角形
分析：求出CD，然后求出∠CAD的正弦、余弦函数值，然后利用二倍角公式求出sin∠BAC的值．
解答：
解：∵Rt△ABC中，∠C是直角，AD是∠BAC的平分线，已知AD=5，AC=4，
∴CD=
=3，∠BAC=2∠CAD，
∴sin∠CAD=
，
cos∠CAD=
，
∴sin∠BAC=2sin∠CADcos∠CAD=2×
×
=
．
∴CD=
| 52-42 |
∴sin∠CAD=
| 3 |
| 5 |
cos∠CAD=
| 4 |
| 5 |
∴sin∠BAC=2sin∠CADcos∠CAD=2×
| 3 |
| 5 |
| 4 |
| 5 |
| 24 |
| 25 |
点评：本题考查解三角形的基本知识，角的平分线的性质以及二倍角公式的应用，考查计算能力．
练习册系列答案
相关题目
两直线3x+y-3=0与ax+2y-1=0垂直，则a=（ ）
| A、-6 | ||
| B、6 | ||
C、-
| ||
D、
|
若△ABC三个内角A、B、C的对边分别为a，b，c，且a=1，∠B=45°，S△ABC=2，则sinA=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|