题目内容
由不等式组
表示的平面区域（图中阴影部分）为（ ）
|
A、 |
B、 |
C、 |
D、 |
考点：二元一次不等式（组）与平面区域
专题：不等式的解法及应用
分析：根据不等式组和平面区域的关系即可得到结论．
解答：
解：由不等式组可知，平面区域位于直线x=0的右侧，y=0的上方，
直线x+y-1=0的下方，
故对应的平面区域为D，
故选：D．
直线x+y-1=0的下方，
故对应的平面区域为D，
故选：D．
点评：本题主要考查二元一次不等式表示平面区域，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
已知集合A={x|3x≤81}，B=（-∞，a），若A∪B=B，则实数a的取值范围是（ ）
| A、[4，+∞） |
| B、（0，4] |
| C、（4，+∞） |
| D、（2，+∞） |
设点O是面积为4的△ABC内部一点，且有
+
+2
=
，则△AOC的面积为（ ）
| OA |
| OB |
| OC |
| 0 |
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
如果复数z=2-ai满足条件|z-1|＜2，那么实数a的取值范围为（ ）
A、（-2
| ||||
| B、（-2，2） | ||||
| C、（-1，1） | ||||
D、（-
|
已知c＞0且c≠1，设命题p：函数f（x）=logcx为减函数，命题q：函数g（x）=x+
＞
（x∈[
，2]）恒成立，若p且q为假命题，p或q为真命题，则实数c的取值范围为（ ）
| 1 |
| x |
| 1 |
| c |
| 1 |
| 2 |
A、（0，
| ||
| B、（1，+∞） | ||
C、（0，
| ||
D、（0，
|
直线3x+2y+a=0在y轴上的截距为（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、
|
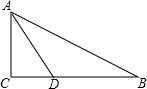如图，Rt△ABC中，∠C是直角，AD是∠BAC的平分线，已知AD=5，AC=4，求sin∠BAC的值．