题目内容
A、B两站相距7.2km，一辆列车从A站开往B站，列车开出t1 s后到达途中C点，这一段速度为1.2t m/s，到C点速度达24m/s，从C点到B站前的D点以等速行驶，从D点开始刹车，经t2 s后，速度为（24-1.2t）m/s．在B点恰好停车，试求：
（1）C，D间的距离；
（2）电车从A站到B站所需的时间．
（1）C，D间的距离；
（2）电车从A站到B站所需的时间．
考点：定积分的简单应用,定积分
专题：导数的综合应用
分析：根据电车的速度变化求出相应的时间，利用积分的意义，求出相应的路程，即可得到结论．
解答：
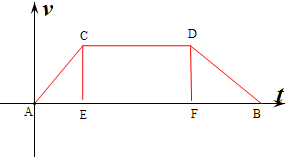解：（1）∵A站开往B站的速度v=1.2t，
∴由1.2t=24，解得t=20，
即AE=20s，
从D点开始刹车，经t2 s后，速度为（24-1.2t）m/s．在B点恰好停车，
则由24-1.2t=0，解得t=20s，即FB=20，
根据积分的几何意义可知AC的路程为
1.2tdt=0.6t2
=240m，
BD的路程为|
(24-1.2t)dt|=|（24t-0.6t2）|
|=240m，
∴CD的距离为720-240-240=240m．
（2）∵C点速度达24 m/s，
∴CD对应的时间t=
=10s，
∴电车从A站到B站所需的时间为20+10+20=50s．
解：（1）∵A站开往B站的速度v=1.2t，∴由1.2t=24，解得t=20，
即AE=20s，
从D点开始刹车，经t2 s后，速度为（24-1.2t）m/s．在B点恰好停车，
则由24-1.2t=0，解得t=20s，即FB=20，
根据积分的几何意义可知AC的路程为
| ∫ | 20 0 |
| | | 20 0 |
BD的路程为|
| ∫ | 20 0 |
20 0 |
∴CD的距离为720-240-240=240m．
（2）∵C点速度达24 m/s，
∴CD对应的时间t=
| 240 |
| 24 |
∴电车从A站到B站所需的时间为20+10+20=50s．
点评：本题主要考查定积分的应用，根据积分的物理意义是解决本题的关键，要求熟练掌握常见函数的积分公式．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
设点O是面积为4的△ABC内部一点，且有
+
+2
=
，则△AOC的面积为（ ）
| OA |
| OB |
| OC |
| 0 |
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
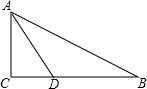如图，Rt△ABC中，∠C是直角，AD是∠BAC的平分线，已知AD=5，AC=4，求sin∠BAC的值．