题目内容
已知f（cosx）=cos17x，求证：f（sinx）=sin17x．
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：将sinx利用诱导公式变形为cos（
-x），利用已知等式变形，再利用诱导公式化简即可得证．
| π |
| 2 |
解答：
解：f（sinx）=f（cos（
-x））=cos[17（
-x）]=cos（
-17x）=cos[8π+（
-17x）]=cos（
-17x）=sin17x．
| π |
| 2 |
| π |
| 2 |
| 17π |
| 2 |
| π |
| 2 |
| π |
| 2 |
点评：此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．
练习册系列答案
相关题目
已知集合A={x|3x≤81}，B=（-∞，a），若A∪B=B，则实数a的取值范围是（ ）
| A、[4，+∞） |
| B、（0，4] |
| C、（4，+∞） |
| D、（2，+∞） |
直线3x+2y+a=0在y轴上的截距为（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、
|
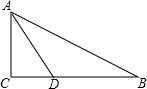如图，Rt△ABC中，∠C是直角，AD是∠BAC的平分线，已知AD=5，AC=4，求sin∠BAC的值．
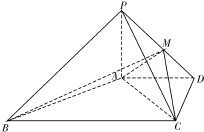如图四棱锥P-ABCD中，PA⊥平面ABCD，AD∥BC，ADCD，且AD=CD=2