题目内容
平面直角坐标系xOy中,椭圆C:
+
=1(a>b>0),椭圆上、下顶点分别为B1,B2.椭圆上异于于B1,B2两点的任一点P满足直线PB1,PB2的斜率之积等于-
,且椭圆的焦距为2
,直线y=kx+2与椭圆交于不同两点S,T.
(Ⅰ)求C的方程;
(Ⅱ)求证:直线B1S与直线B2T的交点在一条定直线上,并求出这条定直线.
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 4 |
| 3 |
(Ⅰ)求C的方程;
(Ⅱ)求证:直线B1S与直线B2T的交点在一条定直线上,并求出这条定直线.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)椭圆方程可化为:
+
=1,设P(x,y),则
+
=1,利用直线PB1,PB2的斜率之积等于-
,可得
•
=-
,即可求C的方程;
(Ⅱ)直线y=kx+2代入椭圆方程,取特殊直线,猜想出定直线,再证明结论即可.
| x2 |
| b2+3 |
| y2 |
| b2 |
| x2 |
| b2+3 |
| y2 |
| b2 |
| 1 |
| 4 |
| y+b |
| x |
| y-b |
| x |
| 1 |
| 4 |
(Ⅱ)直线y=kx+2代入椭圆方程,取特殊直线,猜想出定直线,再证明结论即可.
解答:
解:(I)由已知B1(0,b),B2(0,-b),
∵椭圆的焦距为2
,
∴椭圆方程可化为:
+
=1
设P(x,y),则
+
=1,
∵直线PB1,PB2的斜率之积等于-
,
∴
•
=-
,
∴椭圆方程为
+y2=1 …(4分)
( II)
,可得(1+4k2)x2+16kx+12=0,△>0,可得k2>
.
设S(x1,y1),T(x2,y2),则x1+x2=-
,x1x2=
.
取直线y=x+2与椭圆
+y2=1 交于两点S(-
,
),T(-2,0)
直线B1S:y=
x+1,直线B2T:y=-
x-1,两条直线的交点为Q1(-3,
)
取直线y=-x+2与椭圆
+y2=1交于两点S(
,
),T(2,0)
直线B1S:y=-
x+1,直线B2T:y=
x-1,两条直线的交点为Q2(3,
)
若交点在一条直线上则此直线只能为l:y=
.
设直线直线B1S与直线l:y=
交点为Q0(x0,y0),直线B2T与直线l:y=
交点为Q0′(x0′,y0′),
直线B1S:y=
+1,B2T:y=
-1,
分别令y=
,可得Q0(
•
,
),Q0′(
•
,
),
∴x0-x0′=
••
-
•
=0
∴点Q0(x0,y0)与Q0′(x0′,y0′)重合,
∴交点在直线l:y=
上…(12分)
∵椭圆的焦距为2
| 3 |
∴椭圆方程可化为:
| x2 |
| b2+3 |
| y2 |
| b2 |
设P(x,y),则
| x2 |
| b2+3 |
| y2 |
| b2 |
∵直线PB1,PB2的斜率之积等于-
| 1 |
| 4 |
∴
| y+b |
| x |
| y-b |
| x |
| 1 |
| 4 |
∴椭圆方程为
| x2 |
| 4 |
( II)
|
| 3 |
| 4 |
设S(x1,y1),T(x2,y2),则x1+x2=-
| 16k |
| 1+4k2 |
| 12 |
| 1+4k2 |
取直线y=x+2与椭圆
| x2 |
| 4 |
| 6 |
| 5 |
| 4 |
| 5 |
直线B1S:y=
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
取直线y=-x+2与椭圆
| x2 |
| 4 |
| 6 |
| 5 |
| 4 |
| 5 |
直线B1S:y=-
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 2 |
若交点在一条直线上则此直线只能为l:y=
| 1 |
| 2 |
设直线直线B1S与直线l:y=
| 1 |
| 2 |
| 1 |
| 2 |
直线B1S:y=
| y1-1 |
| x1 |
| y2+1 |
| x2 |
分别令y=
| 1 |
| 2 |
| 1 |
| 2 |
| x1 |
| y1-1 |
| 1 |
| 2 |
| 3 |
| 2 |
| x2 |
| y2+1 |
| 1 |
| 2 |
∴x0-x0′=
| 1 |
| 2 |
| x1 |
| y1-1 |
| 3 |
| 2 |
| x2 |
| y2+1 |
∴点Q0(x0,y0)与Q0′(x0′,y0′)重合,
∴交点在直线l:y=
| 1 |
| 2 |
点评:本题考查椭圆的方程,考查直线与椭圆的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
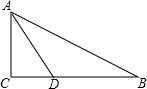 如图,Rt△ABC中,∠C是直角,AD是∠BAC的平分线,已知AD=5,AC=4,求sin∠BAC的值.
如图,Rt△ABC中,∠C是直角,AD是∠BAC的平分线,已知AD=5,AC=4,求sin∠BAC的值.