题目内容
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为
,中奖可以获得2分;方案乙的中奖率为P0(0<P0<1),中奖可以获得3分;未中奖则不得分.每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品.
(Ⅰ)张三选择方案甲抽奖,李四选择方案乙抽奖,记他们的累计得分为X,若X≤3的概率为
,求P0;
(Ⅱ)若张三、李四两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
| 2 |
| 3 |
(Ⅰ)张三选择方案甲抽奖,李四选择方案乙抽奖,记他们的累计得分为X,若X≤3的概率为
| 7 |
| 9 |
(Ⅱ)若张三、李四两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
考点:离散型随机变量的期望与方差
专题:计算题,概率与统计
分析:(Ⅰ)记“这2人的累计得分X≤3”的事件为A,则事件A的对立事件是“X=5”,由题意知,先根据相互独立事件的乘法公式求出对立事件的概率,再利用对立事件的概率公式,结合X≤3的概率为
,即可求P0;
(Ⅱ)设张三、李四两人都选择甲方案抽奖中奖次数为X1,张三、李四两人都选择方案乙抽奖中奖次数为X2,则这两人都选择甲方案抽奖累计得分的数学期望为E(2X1),都选择乙方案抽奖累计得分的数学期望为E(3X2).根据题意知X1~B(2,
),X2~B(2,P0),利用贝努利概率的期望公式计算,再分类讨论,从而得出答案.
| 7 |
| 9 |
(Ⅱ)设张三、李四两人都选择甲方案抽奖中奖次数为X1,张三、李四两人都选择方案乙抽奖中奖次数为X2,则这两人都选择甲方案抽奖累计得分的数学期望为E(2X1),都选择乙方案抽奖累计得分的数学期望为E(3X2).根据题意知X1~B(2,
| 2 |
| 3 |
解答:
解:(Ⅰ)由已知得,张三中奖的概率为
,李四中奖的概率为P0,且两人中奖与否互不影响.
记“这2人的累计得分X≤3”的事件为A,则事件A的对立事件为“X=5”,
因为P(X=5)=
×P0,所以P(A)=1-P(X=5)=1-
×P0=
,
所以P0=
.
(Ⅱ)设张三、李四都选择方案甲抽奖中奖次数为X1,都选择方案乙抽奖中奖次数为X2,
则这两人选择方案甲抽奖累计得分的数学期望为E(2X1),
选择方案乙抽奖累计得分的数学期望为E(3X2).
由已知可得,X1~B(2,
),X2~B(2,P0),
所以E(X1)=2×
=
,E(X2)=2×P0,
从而E(2X1)=2E(X1)=
,E(3X2)=3E(X2)=6P0.
若E(2X1)>E(3X2),则
>6P0,所以0<P0<
;
若E(2X1)<E(3X2),则
<6P0,所以
<P0<1;
若E(2X1)=E(3X2),则
=6P0,所以P0=
.
| 2 |
| 3 |
记“这2人的累计得分X≤3”的事件为A,则事件A的对立事件为“X=5”,
因为P(X=5)=
| 2 |
| 3 |
| 2 |
| 3 |
| 7 |
| 9 |
所以P0=
| 1 |
| 3 |
(Ⅱ)设张三、李四都选择方案甲抽奖中奖次数为X1,都选择方案乙抽奖中奖次数为X2,
则这两人选择方案甲抽奖累计得分的数学期望为E(2X1),
选择方案乙抽奖累计得分的数学期望为E(3X2).
由已知可得,X1~B(2,
| 2 |
| 3 |
所以E(X1)=2×
| 2 |
| 3 |
| 4 |
| 3 |
从而E(2X1)=2E(X1)=
| 8 |
| 3 |
若E(2X1)>E(3X2),则
| 8 |
| 3 |
| 4 |
| 9 |
若E(2X1)<E(3X2),则
| 8 |
| 3 |
| 4 |
| 9 |
若E(2X1)=E(3X2),则
| 8 |
| 3 |
| 4 |
| 9 |
点评:本题考查利用概率知识解决实际问题,考查分类讨论的数学思想,考查数学期望的计算,确定X服从的分布是解题的关键.

练习册系列答案
相关题目
设{an}是公比为正数的等比数列,若a3=4,a7=64,则a8=( )
| A、255 | B、256 |
| C、127 | D、128 |
如果复数z=2-ai满足条件|z-1|<2,那么实数a的取值范围为( )
A、(-2
| ||||
| B、(-2,2) | ||||
| C、(-1,1) | ||||
D、(-
|
直线3x+2y+a=0在y轴上的截距为( )
A、
| ||||
B、-
| ||||
C、
| ||||
D、
|
由a1=1,an+1=
给出的数列{an}的第33项是( )
| an |
| 3an+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
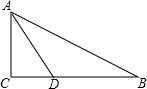 如图,Rt△ABC中,∠C是直角,AD是∠BAC的平分线,已知AD=5,AC=4,求sin∠BAC的值.
如图,Rt△ABC中,∠C是直角,AD是∠BAC的平分线,已知AD=5,AC=4,求sin∠BAC的值.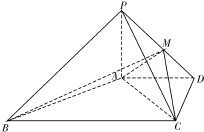 如图四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,ADCD,且AD=CD=2
如图四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,ADCD,且AD=CD=2