题目内容
若△ABC三个内角A、B、C的对边分别为a，b，c，且a=1，∠B=45°，S△ABC=2，则sinA=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：正弦定理
专题：计算题
分析：先利用面积公式求得c的值，进而根据余弦定理求得b，最后根据正弦定理求得sinA．
解答：
解：∵S△ABC=
•a•c•sinB=
•1•c•
=2
∴c=4
∵b=
=
=5
∴根据正弦定理
=
即
=
，求得sinA=
故选：A
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴c=4
| 2 |
∵b=
| a2+c2-2accosB |
1+32-2×1×4
|
∴根据正弦定理
| b |
| sinB |
| a |
| sinA |
即
| 5 | ||||
|
| 1 |
| sinA |
| ||
| 10 |
故选：A
点评：本题主要考查了学生正弦定理的应用．正弦定理、余弦定理和三角形的面积公式是解三角形的常用工具，应熟练掌握．
练习册系列答案
相关题目
已知全集U=R，集合A={x|lgx≤0}，B={x|2x≤1}，则A∪B=（ ）
| A、（-∞，0] |
| B、（-∞，1] |
| C、[0，+∞） |
| D、[1，+∞） |
设点O是面积为4的△ABC内部一点，且有
+
+2
=
，则△AOC的面积为（ ）
| OA |
| OB |
| OC |
| 0 |
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
已知c＞0且c≠1，设命题p：函数f（x）=logcx为减函数，命题q：函数g（x）=x+
＞
（x∈[
，2]）恒成立，若p且q为假命题，p或q为真命题，则实数c的取值范围为（ ）
| 1 |
| x |
| 1 |
| c |
| 1 |
| 2 |
A、（0，
| ||
| B、（1，+∞） | ||
C、（0，
| ||
D、（0，
|
直线3x+2y+a=0在y轴上的截距为（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、
|
如图所示，PA⊥平面ABCD，ABCD是矩形，AB=1，AD=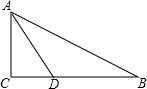
如图，Rt△ABC中，∠C是直角，AD是∠BAC的平分线，已知AD=5，AC=4，求sin∠BAC的值．