题目内容
如果函数y=|x-1|的图象与曲线C：（x-1）2+（y-2）2=λ恰好有两个不同的公共点，则实数λ的取值范围为 ．
考点：直线与圆的位置关系
专题：直线与圆
分析：根据题意画出函数y=|x-1|与曲线C：x2+y2=λ的图象，抓利用数形结合，即可确定出所有满足题意λ的范围．
解答：
解：画出函数y=|x-1|与曲线C：x2+y2=λ的图象，如图所示，
则函数y=|x-1|关于x=1对称，圆心C（1，2），半径R=
，λ＞0，
当射线与圆O相切时两函数图象恰好有两个不同的公共点，
此时圆心到直线y=x-1，即x-y-1=0的距离d=
=
=
=
，解得λ=2，
当圆O半径大于2，即λ＞4时，两函数图象恰好有两个不同的公共点，
综上，实数λ的取值范围是{2}∪（4，+∞）．
故答案为：{2}∪（4，+∞）．
解：画出函数y=|x-1|与曲线C：x2+y2=λ的图象，如图所示，则函数y=|x-1|关于x=1对称，圆心C（1，2），半径R=
| λ |
当射线与圆O相切时两函数图象恰好有两个不同的公共点，
此时圆心到直线y=x-1，即x-y-1=0的距离d=
| |1-2-1| | ||
|
| 2 | ||
|
| 2 |
| λ |
当圆O半径大于2，即λ＞4时，两函数图象恰好有两个不同的公共点，
综上，实数λ的取值范围是{2}∪（4，+∞）．
故答案为：{2}∪（4，+∞）．
点评：此题考查了直线与圆相交的性质，利用了数形结合的思想，灵活运用数形结合思想是解本题的关键．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
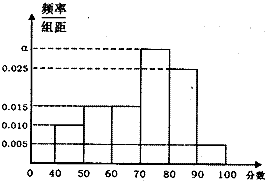某校从参加高三年级期中考试的学生中随机抽出60名学生，将其中考试的政治成绩（均为整数）分成六段[40，50），[50，60），…，[90，100]后得到如下部分频率分布直方图．
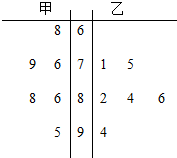在科普知识竞赛前的培训活动中，将甲、乙两名学生的6次培训成绩（百分制）制成如图所示的茎叶图：把一颗骰子投掷两次，第一次出现的点数记为m，第二次出现的点数记为n，则3m≠2n的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|