题目内容
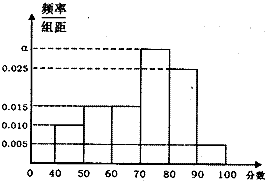 某校从参加高三年级期中考试的学生中随机抽出60名学生,将其中考试的政治成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.
某校从参加高三年级期中考试的学生中随机抽出60名学生,将其中考试的政治成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到如下部分频率分布直方图.(Ⅰ)求分数在[70,80)内的人数;
(Ⅱ)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样本看成一个总体,从中任意选取2人,求其中恰有1人的分数不低于90分的概率.
考点:列举法计算基本事件数及事件发生的概率,频率分布直方图
专题:概率与统计
分析:(Ⅰ)由题意可知分数在[70,80)内的频率为0.3,可得分数在[70,80)内的人数;
(Ⅱ)可得用分层抽样的方法在分数段为[80,100)的学生中抽取一个容量为6的样本,需从[80,90)分数段抽取5人,分别记为a,b,c,d,从[90,100)分数段抽取1人,记为m,列举可得.
(Ⅱ)可得用分层抽样的方法在分数段为[80,100)的学生中抽取一个容量为6的样本,需从[80,90)分数段抽取5人,分别记为a,b,c,d,从[90,100)分数段抽取1人,记为m,列举可得.
解答:
解:(Ⅰ)由题意可知分数在[70,80)内的频率为:
1-(0.010+0.015+0.015+0.025+0.005)×10=1-0.7=0.3,
∴分数在[70,80)分数段的人数为:0.3×60=18人;
(Ⅱ)由题意[80,90)分数段的人数为0.25×60=15,[90,100)分数段的人数为0.05×60=3,
∵用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,
∴需从[80,90)分数段抽取
×6=5人,分别记为a,b,c,d,
从[90,100)分数段抽取
×3=1人,记为m,
设从样本中任取2人,恰有1人的分数不低于90分为事件A,
则所有基本事件有:(a,b),(a,c),(a,d),(a,e),(a,m),(b,c),(b,d),(b,e),(b,m),(c,d),(c,e),(c,m),(d,e)、(d,m),(e,m)共15种,
其中事件A包含的基本事件有:(a,m)、(b,m)、(c,m)、(d,m)、(e,m)共5种,
∴恰有1人的分数不低于90分的概率P(A)=
=
1-(0.010+0.015+0.015+0.025+0.005)×10=1-0.7=0.3,
∴分数在[70,80)分数段的人数为:0.3×60=18人;
(Ⅱ)由题意[80,90)分数段的人数为0.25×60=15,[90,100)分数段的人数为0.05×60=3,
∵用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,
∴需从[80,90)分数段抽取
| 15 |
| 18 |
从[90,100)分数段抽取
| 15 |
| 18 |
设从样本中任取2人,恰有1人的分数不低于90分为事件A,
则所有基本事件有:(a,b),(a,c),(a,d),(a,e),(a,m),(b,c),(b,d),(b,e),(b,m),(c,d),(c,e),(c,m),(d,e)、(d,m),(e,m)共15种,
其中事件A包含的基本事件有:(a,m)、(b,m)、(c,m)、(d,m)、(e,m)共5种,
∴恰有1人的分数不低于90分的概率P(A)=
| 5 |
| 15 |
| 1 |
| 3 |
点评:本题考查古典概型及其概率公式,涉及频率分布直方图,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目