题目内容
某学校组织了一次安全知识竞赛,现随机抽取20名学生的测试成绩,如下表所示(不低于90分的测试成绩称为“优秀成绩”):
(Ⅰ)若从这20人中随机选取3人,求至多有1人是“优秀成绩”的概率;
(Ⅱ)以这20人的样本数据来估计整个学校的总体数据,若从该校全体学生中(人数很多)任选3人,记ξ表示抽到“优秀成绩”学生的人数,求ξ的分布列及数学期望.
| 79 | 90 | 82 | 80 | 84 | 95 | 79 | 86 | 89 | 91 |
| 97 | 86 | 79 | 78 | 86 | 77 | 87 | 89 | 83 | 85 |
(Ⅱ)以这20人的样本数据来估计整个学校的总体数据,若从该校全体学生中(人数很多)任选3人,记ξ表示抽到“优秀成绩”学生的人数,求ξ的分布列及数学期望.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:
分析:(Ⅰ)从这20人中随机选取3人共有
种不同情况,其中至多有1人是“优秀成绩”包括没有“优秀成绩”和有1个“优秀成绩”,利用排列组合公式,求出满足条件的情况个数,代入古典概型公式,可得答案.
(Ⅱ)抽到“优秀成绩”学生的概率P=
,而ξ可以取0,1,2,3,利用独立事件概率公式,可求出ξ的分布列,代入数学期望公式,可得答案.
| C | 3 20 |
(Ⅱ)抽到“优秀成绩”学生的概率P=
| 1 |
| 5 |
解答:
解:(Ⅰ)由表知:“优秀成绩”有4人,
设“从这20人中随机选取3人,至多有1人是“优秀成绩””为事件A
则P(A)=
+
=
. …(5分)
(Ⅱ)由样本估计总体可知抽到“优秀成绩”学生的概率P=
. …(6分)
ξ可以取0,1,2,3 …(7分)
P(ξ=0)=
(
)0(
)3=
;P(ξ=1)=
•
•(
)2=
;
P(ξ=2)=
•(
)2•
=
;P(ξ=3)=
•(
)3•(
)0=
.
ξ的分布列:
∴E(ξ)=0×
+1×
+2×
+3×
=
…(12分)
设“从这20人中随机选取3人,至多有1人是“优秀成绩””为事件A
则P(A)=
| ||
|
| ||||
|
| 52 |
| 57 |
(Ⅱ)由样本估计总体可知抽到“优秀成绩”学生的概率P=
| 1 |
| 5 |
ξ可以取0,1,2,3 …(7分)
P(ξ=0)=
| C | 0 3 |
| 1 |
| 5 |
| 4 |
| 5 |
| 64 |
| 125 |
| C | 1 3 |
| 1 |
| 5 |
| 4 |
| 5 |
| 48 |
| 125 |
P(ξ=2)=
| C | 2 3 |
| 1 |
| 5 |
| 4 |
| 5 |
| 12 |
| 125 |
| C | 3 3 |
| 1 |
| 5 |
| 4 |
| 5 |
| 1 |
| 125 |
ξ的分布列:
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 64 |
| 125 |
| 48 |
| 125 |
| 12 |
| 125 |
| 1 |
| 125 |
| 3 |
| 5 |
点评:本题考查的知识点是离散型随机变量的期望,古典概型,是概率与统计的综合应用,难度中档.

练习册系列答案
相关题目
已知sinα+cosα=-
,求tanα+
=( )
| 2 |
| 1 |
| tanα |
| A、2 | B、1 | C、-1 | D、-2 |
设函数f(x)是R上以4为周期的可导偶函数,则曲线y=f(x)在x=4处的切线的斜率为( )
A、-
| ||
| B、0 | ||
C、
| ||
| D、4 |
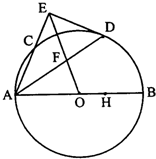 如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于D,DE⊥AC,交AC的延长线于E,OE交AD于F.
如图,AB是⊙O的直径,AC是弦,∠BAC的平分线交⊙O于D,DE⊥AC,交AC的延长线于E,OE交AD于F. 运行如图所示的程序框图,若输出的y值的范围是[0,10],则输入的x的值的范围是
运行如图所示的程序框图,若输出的y值的范围是[0,10],则输入的x的值的范围是 如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆O的切线l,则点A到直线l的距离AD=
如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,过C作圆O的切线l,则点A到直线l的距离AD=