题目内容
袋中有大小相同的五个小球,编号分别为l,2,3,4,5,从袋中每次任取一个球,记下其编号.若所取球的编号为奇数,则把该球编号改为6后放回袋中,继续取球;若所取球的编号为偶数,则直接放回袋中,继续取球.
(Ⅰ)求第二次取到编号为偶数球的概率.
(Ⅱ)求两次取出的球的编号之差的绝对值小于2的概率.
(Ⅰ)求第二次取到编号为偶数球的概率.
(Ⅱ)求两次取出的球的编号之差的绝对值小于2的概率.
考点:离散型随机变量的期望与方差,古典概型及其概率计算公式
专题:综合题,概率与统计
分析:(Ⅰ)利用列举法确定基本事件的个数,利用古典概型的概率公式可得结论;
(Ⅱ)确定两次取出的球的编号之差的绝对值小于2基本事件的个数,利用古典概型的概率公式可得结论.
(Ⅱ)确定两次取出的球的编号之差的绝对值小于2基本事件的个数,利用古典概型的概率公式可得结论.
解答:
解:由题意,从5个球中每次任取一个球,共取2次,满足条件的结果有(1,2),(1,3),(1,4),(1,5),(1,6),(2,1),(2,2),(2,3),(2,4),(2,5),(3,1),(3,2),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(5,1),(5,2),(5,3),(5,4),(5.6)共25个.
(Ⅰ)第二次取到编号为偶数球:(1,2),(1,4),(1,6),(2,2),(2,4),(3,2),(3,4),(3,6),(4,2),(4,4),(5,2),(5,4),(5,6)共13个,
故所求的概率为P=
;
(Ⅱ)两次取出的球的编号之差的绝对值小于2:(1,2),(2,1),(2,2),(2,3),(3,2),(3,4),(4,3),(4,4),(4,5),(5,4),(5,6)共11个,
故所求的概率为P′=
.
(Ⅰ)第二次取到编号为偶数球:(1,2),(1,4),(1,6),(2,2),(2,4),(3,2),(3,4),(3,6),(4,2),(4,4),(5,2),(5,4),(5,6)共13个,
故所求的概率为P=
| 13 |
| 25 |
(Ⅱ)两次取出的球的编号之差的绝对值小于2:(1,2),(2,1),(2,2),(2,3),(3,2),(3,4),(4,3),(4,4),(4,5),(5,4),(5,6)共11个,
故所求的概率为P′=
| 11 |
| 25 |
点评:本题考查概率的计算,考查古典概型的概率公式,利用列举法确定基本事件的个数是关键.

练习册系列答案
相关题目
函数y=Acos(ωx+φ)+b(A>0)的最大值为5,最小值为1,则A=( )
| A、1 | B、2 | C、3 | D、4 |
执行如图所示的程序框图所表示的程序,则输出的结果为( )


| A、9 | B、10 | C、11 | D、13 |
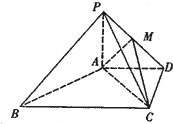 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,PB⊥AC,AD⊥CD,且AD=CD=2
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,PB⊥AC,AD⊥CD,且AD=CD=2