题目内容
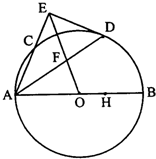如图，AB是⊙O的直径，AC是弦，∠BAC的平分线交⊙O于D，DE⊥AC，交AC的延长线于E，OE交AD于F．（1）求证：DE是⊙O的切线；
（2）若AC=4，AB=10，求
| AF |
| DE |
考点：与圆有关的比例线段,圆的切线的判定定理的证明
专题：
分析：（1）连接OD，根据角平分线定义和等腰三角形性质推行∠CAD=∠ODA，推出OD∥AE，根据平行线性质和切线的判定推出即可；
（2）过D作DH⊥AB于H，则有∠DOH=∠CAB，由△AED≌△AHD可得AE=AH=7，由△AEF和△OFD相似，得出比例式，代入求出即可．
（2）过D作DH⊥AB于H，则有∠DOH=∠CAB，由△AED≌△AHD可得AE=AH=7，由△AEF和△OFD相似，得出比例式，代入求出即可．
解答：
（1）证明：连结OD，可得∠ODA=∠OAD=∠DAC．
∴OD∥AE．
又AE⊥DE，∴OE⊥OD，
又OD为半径．
∴DE是的⊙O切线．…（5分）
（2）解：过D作DH⊥AB于H，
则有∠DOH=∠CAB．
cos∠DOH=cos∠CAB=
=
．…（6分）
∵OD=5，AB=10，OH=2，∴AH=7．
由△AED≌△AHD可得AE=AH=7，…（8分）
又由△AEF∽△DOF，可得AF：DF=AE：OD=7：5，
∴
=
．…（10分）
（1）证明：连结OD，可得∠ODA=∠OAD=∠DAC．∴OD∥AE．
又AE⊥DE，∴OE⊥OD，
又OD为半径．
∴DE是的⊙O切线．…（5分）
（2）解：过D作DH⊥AB于H，
则有∠DOH=∠CAB．
cos∠DOH=cos∠CAB=
| AC |
| AB |
| 2 |
| 5 |
∵OD=5，AB=10，OH=2，∴AH=7．
由△AED≌△AHD可得AE=AH=7，…（8分）
又由△AEF∽△DOF，可得AF：DF=AE：OD=7：5，
∴
| AF |
| DF |
| 7 |
| 5 |
点评：本题综合考查了等腰三角形的性质，平行线的性质，切线的性质和判定，相似三角形的性质和判定，锐角三角函数，勾股定理，角平分线定义等知识点的运用，题目较好，综合性强，有一定的难度，主要培养学生综合运用所学知识进行推理的能力．
练习册系列答案
相关题目
设函数f（x）=|lnx|，则下列结论中正确的是（ ）
A、f（1）＜f（
| ||
B、f（
| ||
C、f（e）＜f（1）＜f（
| ||
D、f（e）＜f（
|
关于x的不等式ax2+2ax-4＜0对一切x∈R恒成立，则a的取值范围是（ ）
| A、（-4，0） |
| B、（-4，0] |
| C、[-4，0） |
| D、[-4，0] |
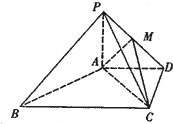如图，在四棱锥P-ABCD中，PA⊥平面ABCD，AD∥BC，PB⊥AC，AD⊥CD，且AD=CD=2