题目内容
已知函数f(x)=(1-x)ex-1.
(Ⅰ)求函数f(x)的最大值;
(Ⅱ)若x≥0时,g(x)=f(x)+λx2≤0,求λ的取值范围.
(Ⅰ)求函数f(x)的最大值;
(Ⅱ)若x≥0时,g(x)=f(x)+λx2≤0,求λ的取值范围.
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(Ⅰ)求最值实质就是利用导数判断函数的单调性,转化为导函数的问题,
(Ⅱ)先求得g′(x),然后对参数λ进行分类讨论.
(Ⅱ)先求得g′(x),然后对参数λ进行分类讨论.
解答:
解:(Ⅰ)∵f(x)=(1-x)ex-1.
∴f′(x)=-xex,
当x=0时,f′(x)=0;当x<0时,f′(x)>0;当x>0时,f′(x)<0;
所以函数f(x)在区间(-∞,0)上单调递增,在区间(0,+∞)上单调递减;
故f(x)max=f(0)=0.
(Ⅱ)由g(x)=(1-x)e2+λx2-1,得g′(x)=-x(ex-2λ).
当λ≤0时,由(Ⅰ)得g(x)=f(x)+λx2≤f(x)≤0成立;
当0<λ≤
时,因为x∈(0,+∞)时g′(x)<0,所以x≥0时,
g(x)≤g(0)=0成立;
当λ>
时,因为x∈(0,ln2λ)时,g′(x)>0,所以g(x)>g(0)=0.
综上,知λ的取值范围是(-∞,
].
∴f′(x)=-xex,
当x=0时,f′(x)=0;当x<0时,f′(x)>0;当x>0时,f′(x)<0;
所以函数f(x)在区间(-∞,0)上单调递增,在区间(0,+∞)上单调递减;
故f(x)max=f(0)=0.
(Ⅱ)由g(x)=(1-x)e2+λx2-1,得g′(x)=-x(ex-2λ).
当λ≤0时,由(Ⅰ)得g(x)=f(x)+λx2≤f(x)≤0成立;
当0<λ≤
| 1 |
| 2 |
g(x)≤g(0)=0成立;
当λ>
| 1 |
| 2 |
综上,知λ的取值范围是(-∞,
| 1 |
| 2 |
点评:本题主要考查了函数的最值得求法,以及求参数的取值范围,关键是求导.

练习册系列答案
相关题目
设ab>0,下面四个不等式中,正确的是( )
①|a+b|>|a|;②|a+b|<|b|;③|a+b|<|a-b|;④|a+b|>|a|-|b|
①|a+b|>|a|;②|a+b|<|b|;③|a+b|<|a-b|;④|a+b|>|a|-|b|
| A、①和② | B、①和③ |
| C、①和④ | D、②和④ |
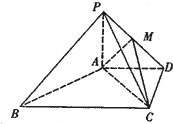 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,PB⊥AC,AD⊥CD,且AD=CD=2
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,PB⊥AC,AD⊥CD,且AD=CD=2