题目内容
14.已知f(x)=|ax+1|(a∈R),不等式f(x)≤3的解集为{x|-2≤x≤1}.(Ⅰ)求a的值;
(Ⅱ)若f(x)-2f($\frac{x}{2}$)≤k恒成立,求k的取值范围.
分析 (Ⅰ)由条件分类讨论,解绝对值不等式,求得不等式f(x)≤3的解集.再根据不等式f(x)≤3的解集为{x|-2≤x≤1},求得a的值.
(Ⅱ)由题意可得|2x+1|-2|x+1|≤k恒成立,令g(x)=|2x+1|-2|x+1|,利用分段函数求得g(x)的最大值,可得k的范围.
解答 解:(Ⅰ)不等式f(x)≤3,即|ax+1|≤3,即-3≤ax+1≤3,即-4≤ax≤2.
当a>0时,求得-$\frac{4}{a}$≤x≤$\frac{2}{a}$,再根据它的解集为{x|-2≤x≤1},可得$\left\{\begin{array}{l}{-\frac{4}{a}=-2}\\{\frac{2}{a}=1}\end{array}\right.$,求得a=2.
当a<0时,求得$\frac{2}{a}$≤x≤-$\frac{4}{a}$,再根据它的解集为{x|-2≤x≤1},可得$\left\{\begin{array}{l}{\frac{2}{a}=-2}\\{-\frac{4}{a}=1}\end{array}\right.$,a无解.
综上可得,a=2,f(x)=|2x+1|.
(Ⅱ)若f(x)-2f($\frac{x}{2}$)≤k恒成立,即|2x+1|-2|x+1|≤k恒成立.
令g(x)=|2x+1|-2|x+1|=$\left\{\begin{array}{l}{1,x<-1}\\{-3x-3,-1≤x≤-\frac{1}{2}}\\{-1,x>-\frac{1}{2}}\end{array}\right.$,故函数g(x)的最大值为1,
故k≥1.
点评 本题主要考查绝对值不等式的解法,函数的恒成立问题,分段函数的应用,求函数的最值,属于中档题.

练习册系列答案
相关题目
4.在等比数列{an}中,已知a1=1,a3=2a2,则该数列前6项和S6=( )
| A. | 31 | B. | 63 | C. | 127 | D. | 176 |
2.下列各式中,正确的是( )
| A. | sin(-$\frac{π}{8}$)>sin(-$\frac{π}{10}$) | B. | cos(-$\frac{23π}{5}$)>cos(-$\frac{17π}{4}$) | ||
| C. | cos250°>cos260° | D. | tan144°<tan148° |
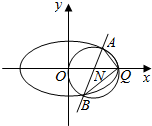 如图,已知焦点在x轴上的椭圆C过点(-2,0),且离心率为$\frac{\sqrt{3}}{2}$,Q为椭圆C的右顶点.
如图,已知焦点在x轴上的椭圆C过点(-2,0),且离心率为$\frac{\sqrt{3}}{2}$,Q为椭圆C的右顶点.