题目内容
12.若对任意的x≥2,都有(x+a)|x+a|+(ax)|x|≤0,则a的最大值为-1.分析 由题意可得,x≥2时,(x+a)|x+a|+(ax)•x≤0恒成立,分类讨论,求得a的范围,可得a的最大值.
解答 解:对任意的x≥2,都有(x+a)|x+a|+(ax)|x|≤0,即 x≥2时,(x+a)|x+a|+(ax)•x≤0恒成立.
①若x+a≥0,即a≥-2时,则有(x+a)2+ax2≤0,
∴(a+1)x2+2ax+a2≤0.
令f(x)=(a+1)x2+2ax+a2,则有a+1=0,或-$\left\{\begin{array}{l}{a+1<0}\\{-\frac{2a}{2(a+1)}<2}\\{f(2)=4(a+1)+4a+{a}^{2}≤0}\end{array}\right.$,
求得a=-1,或-4-2$\sqrt{3}$≤a≤-4+2$\sqrt{3}$,综合可得-4-2$\sqrt{3}$≤a≤-2 或a=-1.
②若x+a<0,即a<-2时,则有-(x+a)2+ax2≤0,
∴(a-1)x2-2ax-a2≤0.
令g(x)=(a-1)x2-2ax-a2,则它的图象的对称轴为x=$\frac{a}{a-1}$<0,g(2)=-4-a2≤0恒成立.
即此时,a的范围为 a<-2.
③若x+a=0,即a=-x≤-2 时,则由题意可得ax2≤0,满足条件.
综合①②③可得,a≤-2或-4-2$\sqrt{3}$≤a≤-2 或a=-1,故a的最大值为-1,
故答案为:-1.
点评 本题主要考查绝对值不等式的解法,分段函数的应用,二次函数的性质,属于难题.

练习册系列答案
相关题目
3.已知G,N,P在△ABC所在平面内,a,b,c分别为角A,B,C所对的边,且分别满足$\overrightarrow{GA}$+$\overrightarrow{GB}$+$\overrightarrow{GC}$=$\overrightarrow{0}$,sin2A•$\overrightarrow{NA}$+sin2B•$\overrightarrow{NB}$+sin2C•$\overrightarrow{NC}$=$\overrightarrow{0}$,a$\overrightarrow{PA}$+b$\overrightarrow{PB}$+c$\overrightarrow{PC}$=$\overrightarrow 0$,则点G,N,P依次是△ABC的( )
| A. | 重心,外心,内心 | B. | 重心,垂心,内心 | C. | 重心,垂心,外心 | D. | 内心,外心,重心 |
7.某班为了调查同学们周末的运动时间,随机对该班级50名同学进行了不记名的问卷调查,得到了如下表所示的统计结果:
(1)根据统计结果,能否在犯错误概率不超过0.05的前提下,认为该班同学周末的运动时间与性别有关?
(2)用分层抽样的方法,从男生中抽取6名同学,再从这6名同学中随机抽取2名同学,求这两名同学中恰有一位同学运动时间超过2小时的概率.
附:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 运动时间不超过2小时 | 运动时间超过2小时 | 合计 | |
| 男生 | 10 | 20 | 30 |
| 女生 | 13 | 7 | 20 |
| 合计 | 23 | 27 | 50 |
(2)用分层抽样的方法,从男生中抽取6名同学,再从这6名同学中随机抽取2名同学,求这两名同学中恰有一位同学运动时间超过2小时的概率.
附:K2=$\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
2.为了调整个人所得税征收制度,某机构准备调查了解某市市民的收人情况,随机抽取了n名市民进行试点凋查,其月收人介于1200元和4200元之间,将调查结果按如下方式分为五组:第一组[1200,1800):第二组[1800,2400)…:第五组[3600,4200].下表是按上述分组方式得到的频率分布表:
(I)求n及上表中的x,y,z,a,b的值;
(Ⅱ)为了了解市民对个人所得税征收制度的意见,现利用分层抽样的方法从这n名市民中抽取一个容量为50的样本进行问卷凋查,若从第一组或第五组中抽取的市民中任选两名,求事件“两人收入之差大于1000元”的概率.
| 分组 | 频数 | 频率 |
| [1200,1800) | x | A |
| [1800,2400) | 90 | B |
| [2400,3000) | y | 0.40 |
| [3000,3600) | 160 | 0.32 |
| [3600,4200] | z | 0.04 |
(Ⅱ)为了了解市民对个人所得税征收制度的意见,现利用分层抽样的方法从这n名市民中抽取一个容量为50的样本进行问卷凋查,若从第一组或第五组中抽取的市民中任选两名,求事件“两人收入之差大于1000元”的概率.
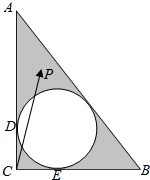 在Rt△ABC中,∠C是直角,CA=4,CB=3,△ABC的内切圆交CA,CB于点D,E,点P是图中阴影区域内的一点(不包含边界).若$\overrightarrow{CP}$=x$\overrightarrow{CD}$+y$\overrightarrow{CE}$,则x+y的值可以是( )
在Rt△ABC中,∠C是直角,CA=4,CB=3,△ABC的内切圆交CA,CB于点D,E,点P是图中阴影区域内的一点(不包含边界).若$\overrightarrow{CP}$=x$\overrightarrow{CD}$+y$\overrightarrow{CE}$,则x+y的值可以是( )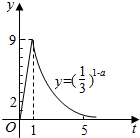 我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线
我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线