题目内容
14.已知sin(3π+α)=lg$\frac{1}{\root{3}{10}}$,求$\frac{cos(π+α)}{cosα[cos(π-α)-1]}$+$\frac{cos(α-2π)}{cosαcos(π-α)+cos(-α)}$的值.分析 先化简已知:利用诱导公式sin(π+α)=-sinα化简等式左边,然后利用对数定义lg$\frac{1}{\root{3}{10}}$=lg10${\;}^{-\frac{1}{3}}$=-$\frac{1}{3}$得到sinα的值;再化简原式:利用cos(π+α)=-cosα,cos(π-α)=cosα,cos(2π-α)=cosα及同角三角函数间的基本关系进行化简,将sinα的值代入即可求出.
解答 解:∵由于sin(3π+α)=-sinα,lg$\frac{1}{\root{3}{10}}$=lg10${\;}^{-\frac{1}{3}}$=-$\frac{1}{3}$,得sinα=$\frac{1}{3}$,
∴原式=$\frac{-cosα}{cosα(-cosα-1)}$+$\frac{cosα}{-co{s}^{2}α+cosα}$=$\frac{1}{1+cosα}$+$\frac{1}{1-cosα}$=$\frac{2}{sin2α}$=18.
点评 本题主要考查学生灵活运用诱导公式进行化简求值,会根据对数的定义求对数的值,灵活运用同角三角函数间的基本关系化简求值,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
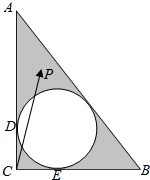 在Rt△ABC中,∠C是直角,CA=4,CB=3,△ABC的内切圆交CA,CB于点D,E,点P是图中阴影区域内的一点(不包含边界).若$\overrightarrow{CP}$=x$\overrightarrow{CD}$+y$\overrightarrow{CE}$,则x+y的值可以是( )
在Rt△ABC中,∠C是直角,CA=4,CB=3,△ABC的内切圆交CA,CB于点D,E,点P是图中阴影区域内的一点(不包含边界).若$\overrightarrow{CP}$=x$\overrightarrow{CD}$+y$\overrightarrow{CE}$,则x+y的值可以是( )