题目内容
（
-2）6的展开式中x2的系数是（ ）
| x |
| A、-120 | B、120 |
| C、-60 | D、60 |
考点：二项式系数的性质
专题：二项式定理
分析：先求得二项式展开式的通项公式，再令x的幂指数等于2，求得r的值，即可求得含x2的项的系数．
解答：
解：（
-2）6的展开式的通项公式为Tr+1=
•（-2）r•x
，
令
=2，求得 r=2，可得展开式中x2的系数是
•4=60，
故选：D．
| x |
| C | r 6 |
| 6-r |
| 2 |
令
| 6-r |
| 2 |
| C | 2 6 |
故选：D．
点评：本题主要考查二项式定理的应用，二项式展开式的通项公式，求展开式中某项的系数，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
若0＜a＜1，则下列各式中正确的是（ ）
| A、loga（1-a）＞0 |
| B、a1-a＞1 |
| C、loga（1-a）＜0 |
| D、（1-a）2＞a2 |
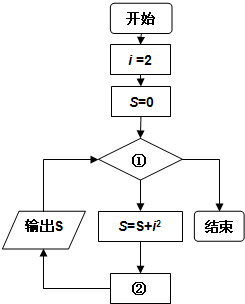如图是表示输出22，22+42，22+42+62，…，22+42+62+…+20042的值的过程的一个程序框图，那么在图中①、②处应分别填上（ ）| A、i≤2014，i=i+2 |
| B、i≤1007，i=i+2 |
| C、i≤2014，i=i+1 |
| D、i≤1007，i=i+1 |
若直线l上不同的三个点A，B，C与直线l外一点O，使得x2
+x
=2
成立，则满足条件的实数x的集合为（ ）
| OA |
| OB |
| BC |
| A、{-1，0} | ||||||||
B、{
| ||||||||
C、{
| ||||||||
| D、{-1} |
如果
+
=1表示焦点在x轴上的椭圆，则实数a的取值范围为（ ）
| x2 |
| a2 |
| y2 |
| a+2 |
| A、（-2，+∞） |
| B、（-2，-1）∪（2，+∞） |
| C、（-∞，-1）∪（2，+∞） |
| D、任意实数R |