Question

13．已知函数y=cosx+2|cosx|，x∈[0，2π]与函数y=k的图象有四个交点，则k∈（0，1）．

Answer 1

分析 画出函数f（x）在x∈[0，2π]以及直线y=k 的图象，数形结合可得k的取值范围．

解答 解：画出函数y=cosx+2|cosx|
=$\left\{\begin{array}{l}{3cosx，x∈[0，\frac{π}{2}]∪[\frac{3π}{2}，2π]}\\{-cosx，x∈（\frac{π}{2}，\frac{3π}{2}）}\end{array}\right.$
以及直线y=k 的图象，如图所示；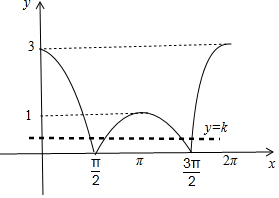

由f（x）的图象与直线y=k有且仅有四个不同的交点，可得0＜k＜1．
故答案为：（0，1）．

点评 本题主要考查余弦函数的图象，体现了数形结合的数学思想，属于基础题．