题目内容
 为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.
为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.(1)求这6位同学成绩的平均数和标准差;
(2)从这6位同学中随机选出两位同学来分析成绩的分布情况,求这两位同学中恰有一位同学成绩低于平均分的概率.
考点:古典概型及其概率计算公式,茎叶图
专题:概率与统计
分析:(1)利用
=
×(76+76+78+78+82+96)与方差的计算公式计算;
(2)根据6名同学中由4人的成绩低于平均分,列举所有的基本事件,找出符合题意得基本事件个数,利用古典概型概率个数计算即可.
. |
| x |
| 1 |
| 6 |
(2)根据6名同学中由4人的成绩低于平均分,列举所有的基本事件,找出符合题意得基本事件个数,利用古典概型概率个数计算即可.
解答:
解:(1)这6位同学的成绩平均数为,
=
×(76+76+78+78+82+96)=81,
又s2=
(xn-
)2
=
(52+52+32+32+12+152)=49.
故这6位问学成绩的标准差为s=7.
(2)从6位同学中随机选取2位同学,
包含的基本事件空间为(76,76)、(76,78)、
(76,78)、(76,82)、(76,96)、(76,78)、(76,78)、(76,82)、(76,96)、(78,78)、
(78,82)、(78,96)、(78,82)、(78,96)、(82,96)15个基本事件.
其中括号内数字分别表示2位同学的成绩.
记“选出的2位问学中,恰有1位同学的成绩低于平均分”为事件A,
则事件A包含的基本事件为(76,82)、(76,96)、(76,82)、(76,96)、
(78,82)、(78,96)、(78,82)、(78,96)共8个基本事件,
则P(A)=
.
故从6位同学中随机选取2位同学,恰有1位同学的成绩低于平均分的概率为
.
. |
| x |
| 1 |
| 6 |
又s2=
| 1 |
| 6 |
| 6 |
 |
| n=1 |
. |
| x |
=
| 1 |
| 6 |
故这6位问学成绩的标准差为s=7.
(2)从6位同学中随机选取2位同学,
包含的基本事件空间为(76,76)、(76,78)、
(76,78)、(76,82)、(76,96)、(76,78)、(76,78)、(76,82)、(76,96)、(78,78)、
(78,82)、(78,96)、(78,82)、(78,96)、(82,96)15个基本事件.
其中括号内数字分别表示2位同学的成绩.
记“选出的2位问学中,恰有1位同学的成绩低于平均分”为事件A,
则事件A包含的基本事件为(76,82)、(76,96)、(76,82)、(76,96)、
(78,82)、(78,96)、(78,82)、(78,96)共8个基本事件,
则P(A)=
| 8 |
| 15 |
故从6位同学中随机选取2位同学,恰有1位同学的成绩低于平均分的概率为
| 8 |
| 15 |
点评:本题考查了由数据的茎叶图求平均数,方差与标准差,考查了利用列举法求古典概型概率的方法.属于基础题.

练习册系列答案
相关题目
已知f(x)是定义在(0,+∞)上的单调函数,f′(x)是f(x)的导函数,若对?x∈(0,+∞),都有f[f(x)-2x]=3,则方程f′(x)-
=0的解所在的区间是( )
| 4 |
| x |
A、(0,
| ||
B、(
| ||
| C、(1,2) | ||
| D、(2,3) |
 如图,延长⊙O的半径OA到B,使OA=AB,DE是圆的一条切线,E是切点,过点B作DE的垂线,垂足为点C.
如图,延长⊙O的半径OA到B,使OA=AB,DE是圆的一条切线,E是切点,过点B作DE的垂线,垂足为点C.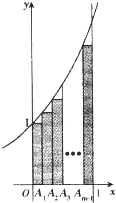 如图.A1,A2,…Am-1(m≥2)将区间[0,l]m等分,直线x=0,x=1,y=0和曲线y=ex所围成的区域为Ω1图中m个矩形构成的阴影区域为Ω2.在Ω1中任取一点,则该点取自Ω2的概率等于
如图.A1,A2,…Am-1(m≥2)将区间[0,l]m等分,直线x=0,x=1,y=0和曲线y=ex所围成的区域为Ω1图中m个矩形构成的阴影区域为Ω2.在Ω1中任取一点,则该点取自Ω2的概率等于