题目内容
当a<0时,函数m(t)=
at2+t-a的定义域为[
,2],记函数m(t)的最大值为g(a).
(1)求g(a)的解析式;
(2)试求满足g(a)>g(
)的所有实数a的值.
| 1 |
| 2 |
| 2 |
(1)求g(a)的解析式;
(2)试求满足g(a)>g(
| 1 |
| a |
考点:函数的最值及其几何意义
专题:分类讨论,数形结合法
分析:(1)二次函数含参讨论单调性,利用性质和单调性解题,(2)利用分类讨论的数学思想求解
解答:
解:(1)a<0,函数图象开口向上,关于直线t=-
对称
当-
≤
即a≤-
时,函数在[
,2]上单调递减,最大值g(a)=m(
)=
,
当
<-
<2即-
<a<-
时,最大值g(a)=m(-
)=-
-
,
当-
≥2即-
≤a<0时,函数在[
,2]上单调递增,最大值g(a)=m(2)=a+2,
综上,g(a)=
(2)当 a≤-
时,函数为常函数,不满足题意,
当-
<a<-
时,得-
-a>-
-
化简得
>0由a<0得a<-1
当-
≤a<0时,得a+2>
+2化简得
>0由a<0得-1<a<0
综上,a<0且a≠-1
| 1 |
| a |
当-
| 1 |
| a |
| 2 |
| ||
| 2 |
| 2 |
| 2 |
| 2 |
当
| 2 |
| 1 |
| a |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| a |
| 1 |
| 2a |
| 1 |
| a |
当-
| 1 |
| a |
| 1 |
| 2 |
| 2 |
综上,g(a)=
|
(2)当 a≤-
| ||
| 2 |
当-
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2a |
| 1 | ||
2×
|
| 1 |
| a |
| 1-a2 |
| 2a |
当-
| 1 |
| 2 |
| 1 |
| a |
| a2-1 |
| a |
综上,a<0且a≠-1
点评:注意分类讨论和函数思想的应用

练习册系列答案
相关题目
已知平面向量
=(1,2),
=(-2,m),且
⊥
,则2
+3
=( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、(8,16) |
| B、(-4,-8) |
| C、(-4,7) |
| D、(8,1) |
设0<a<b,且f(x)=
,则下列大小关系式成立的是( )
1+
| ||
| x |
A、f (a)<f (
| ||||
B、f (
| ||||
C、f (
| ||||
D、f (b)<f (
|
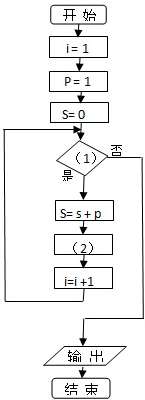 给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.先将右面给出的程序框图补充完整,再将与其功能相当的程序语言补充完整,把答案写在下面空格上.
给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.先将右面给出的程序框图补充完整,再将与其功能相当的程序语言补充完整,把答案写在下面空格上.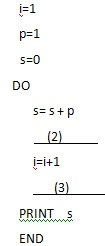

 为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.
为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.