题目内容
有一种新型的洗衣液,特点是去污速度快.已知每投放a(1≤a≤4,且a∈R)个单位的洗衣液,它在水中释放的浓度y与时间x(小时)的关系可近似地表示为:y=a•f(x),其中f(x)=
;若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,只有当水中洗衣液的浓度不低于
时,才能起到有效去污的作用.
(Ⅰ) 如果只投放1个单位的洗衣液,则能够维持有效去污作用的时间有多长?
(Ⅱ) 第一次投放1个单位的洗衣液后,当水中洗衣液的浓度减少到
时,马上再投放1个单位的洗衣液,设第二次投放后水中洗衣液的浓度为g(x),求g(x)的函数解析式及其最大值;
(Ⅲ)若第一次投放2个单位的洗衣液,4小时后再投放a个单位的洗衣液,要使接下来的2小时中能够持续有效去污,试求a的最小值.
|
| 1 |
| 3 |
(Ⅰ) 如果只投放1个单位的洗衣液,则能够维持有效去污作用的时间有多长?
(Ⅱ) 第一次投放1个单位的洗衣液后,当水中洗衣液的浓度减少到
| 1 |
| 3 |
(Ⅲ)若第一次投放2个单位的洗衣液,4小时后再投放a个单位的洗衣液,要使接下来的2小时中能够持续有效去污,试求a的最小值.
考点:导数在最大值、最小值问题中的应用,函数模型的选择与应用
专题:导数的综合应用
分析:(I)利用水中洗衣液的浓度不低于
,可得f(x)≥
,再利用分段函数的意义分类讨论即可解出;
(II)由(I)知,x=4时第二次投入1单位洗衣液,显然g(x)的定义域为{x|4≤x≤10},根据分段函数的意义可得:当4≤x≤6时,第一次投放1单位洗衣液还有残留,故g(x)=(1-
)+[2-
-
]=
-
-
;当6<x≤10时,第一次投放1单位洗衣液已无残留,故当6<x≤7时,g(x)=2-
-
=
-
-
;当7<x≤10时,g(x)=1-
=
-
;再利用函数的单调性即可得出.
(III)当4≤x≤6时,y=2(1-
)+a(2-
-
)=2+
-
x-
,通过对a分类讨论,再研究其单调性最小值即可.
| 1 |
| 3 |
| 1 |
| 3 |
(II)由(I)知,x=4时第二次投入1单位洗衣液,显然g(x)的定义域为{x|4≤x≤10},根据分段函数的意义可得:当4≤x≤6时,第一次投放1单位洗衣液还有残留,故g(x)=(1-
| x |
| 6 |
| x-4 |
| 6 |
| 6 |
| (x-4)+3 |
| 11 |
| 3 |
| x |
| 3 |
| 6 |
| x-1 |
| x-4 |
| 6 |
| 6 |
| x-4+3 |
| 8 |
| 3 |
| x |
| 6 |
| 6 |
| x-1 |
| x-4 |
| 6 |
| 5 |
| 3 |
| x |
| 6 |
(III)当4≤x≤6时,y=2(1-
| x |
| 6 |
| x-4 |
| 6 |
| 6 |
| x-1 |
| 8a |
| 3 |
| a+2 |
| 6 |
| 6a |
| x-1 |
解答:
解:(I)由题意知
或
解得1≤x≤3或3≤x≤4,即1≤x≤4;
∴能够维持有效的抑制作用的时间:4-1=3小时;
(II)由(I)知,x=4时第二次投入1单位洗衣液,显然g(x)的定义域为{x|4≤x≤10};
当4≤x≤6时,第一次投放1单位洗衣液还有残留,故g(x)=(1-
)+[2-
-
]=
-
-
;
当6<x≤10时,第一次投放1单位洗衣液已无残留,故
当6<x≤7时,g(x)=2-
-
=
-
-
;
当7<x≤10时,g(x)=1-
=
-
;
∴g(x)=
.
当4≤x≤6时,g(x)=
-
-
=
-(
+
)≤
-2
=
-2
;
当且仅当
=
时取“=”,即x=1+3
∈[4,6];
当6<x≤10时,第一次投放1单位洗衣液已无残留,
当6<x≤7时,g′(x)=
-
=
>0,∴g(x)为增函数;
当7<x≤10时,g(x)为减函数;故 g(x)max=g(7)=
,
又(
-2
)-
=
=
>0,
∴第一次投放1+3
小时后,水中洗衣液浓度的达到最大值为
-2
;
(III)当4≤x≤6时,
y=2(1-
)+a(2-
-
)
=2+
-
x-
=
-[
(x-1)+
],
若
<a≤4时,u=[
(x-1)+
]max=
∴ymin=
-
=
≥
恒成立;
若1≤a≤
时,u=[
(x-1)+
]max=
∴ymin=
-
=
,
∴由
≥
得a≥
,∴
≤a≤
;
综上,
≤a≤4,即a的最小值为
.
|
|
解得1≤x≤3或3≤x≤4,即1≤x≤4;
∴能够维持有效的抑制作用的时间:4-1=3小时;
(II)由(I)知,x=4时第二次投入1单位洗衣液,显然g(x)的定义域为{x|4≤x≤10};
当4≤x≤6时,第一次投放1单位洗衣液还有残留,故g(x)=(1-
| x |
| 6 |
| x-4 |
| 6 |
| 6 |
| (x-4)+3 |
| 11 |
| 3 |
| x |
| 3 |
| 6 |
| x-1 |
当6<x≤10时,第一次投放1单位洗衣液已无残留,故
当6<x≤7时,g(x)=2-
| x-4 |
| 6 |
| 6 |
| x-4+3 |
| 8 |
| 3 |
| x |
| 6 |
| 6 |
| x-1 |
当7<x≤10时,g(x)=1-
| x-4 |
| 6 |
| 5 |
| 3 |
| x |
| 6 |
∴g(x)=
|
当4≤x≤6时,g(x)=
| 11 |
| 3 |
| x |
| 3 |
| 6 |
| x-1 |
| 10 |
| 3 |
| x-1 |
| 3 |
| 6 |
| x-1 |
| 10 |
| 3 |
|
| 10 |
| 3 |
| 2 |
当且仅当
| x-1 |
| 3 |
| 6 |
| x-1 |
| 2 |
当6<x≤10时,第一次投放1单位洗衣液已无残留,
当6<x≤7时,g′(x)=
| 6 |
| (x-1)2 |
| 1 |
| 6 |
| (x+5)(7-x) |
| 6(x-1)2 |
当7<x≤10时,g(x)为减函数;故 g(x)max=g(7)=
| 1 |
| 2 |
又(
| 10 |
| 3 |
| 2 |
| 1 |
| 2 |
17-12
| ||
| 6 |
| ||||
| 6 |
∴第一次投放1+3
| 2 |
| 10 |
| 3 |
| 2 |
(III)当4≤x≤6时,
y=2(1-
| x |
| 6 |
| x-4 |
| 6 |
| 6 |
| x-1 |
=2+
| 8a |
| 3 |
| a+2 |
| 6 |
| 6a |
| x-1 |
=
| 10+15a |
| 6 |
| a+2 |
| 6 |
| 6a |
| x-1 |
若
| 10 |
| 7 |
| a+2 |
| 6 |
| 6a |
| x-1 |
| 5a+2 |
| 2 |
∴ymin=
| 10+15a |
| 6 |
| 5a+2 |
| 2 |
| 2 |
| 3 |
| 1 |
| 3 |
若1≤a≤
| 10 |
| 7 |
| a+2 |
| 6 |
| 6a |
| x-1 |
| 61a+50 |
| 30 |
∴ymin=
| 10+15a |
| 6 |
| 61a+50 |
| 30 |
| 7a |
| 15 |
∴由
| 7a |
| 15 |
| 1 |
| 3 |
| 5 |
| 7 |
| 5 |
| 7 |
| 10 |
| 7 |
综上,
| 5 |
| 7 |
| 5 |
| 7 |
点评:本题考查了分段函数的意义及其单调性、分类讨论等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
若抛物线C:y2=2px(p>0)上一点到焦点和x轴的距离分别为5和3,则此抛物线的方程为( )
| A、y2=2x | ||
B、y2=(
| ||
| C、y2=2x或y2=18x | ||
D、y2=3x或y2=(
|
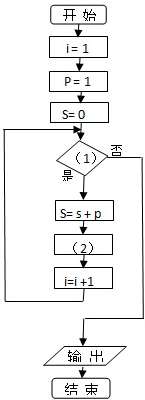 给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.先将右面给出的程序框图补充完整,再将与其功能相当的程序语言补充完整,把答案写在下面空格上.
给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.先将右面给出的程序框图补充完整,再将与其功能相当的程序语言补充完整,把答案写在下面空格上.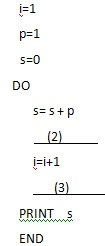
 为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.
为了解某校学生参加某项测试的情况,从该校学生中随机抽取了6位同学,这6位同学的成绩(分数)如茎叶图所示.