题目内容
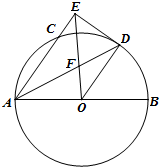如图，已知AB是⊙O的直径，AC是⊙O的弦，∠BAC的平分线AD交⊙O于D，过点D作DE⊥AC交AC的延长线于点E，OE交AD于点F．若| AC |
| AB |
| 3 |
| 5 |
（Ⅰ）求证：OD∥AE；
（Ⅱ）求
| AF |
| FD |
考点：与圆有关的比例线段
专题：推理和证明
分析：（Ⅰ）连接OD，BC，设BC交OD于点M，则∠OAD=∠ODA，从而∠ODA=∠DAE，由此能证明OD∥AE．
（Ⅱ）由已知得四边形CMDE为平行四边形，从而CE=MD，由
=
，设AC=3x，AB=5x，则OM=
x，MD=x，从而AE=AC+CE=4x，由此能求出
的值．
（Ⅱ）由已知得四边形CMDE为平行四边形，从而CE=MD，由
| AC |
| AB |
| 3 |
| 5 |
| 3 |
| 2 |
| AF |
| FD |
解答：
（Ⅰ）证明：连接OD，BC，设BC交OD于点M．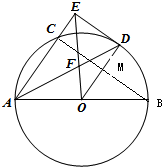
因为OA=OD，所以∠OAD=∠ODA，（2分）
又因为∠OAD=∠DAE，所以∠ODA=∠DAE，
所以OD∥AE．（4分）
（Ⅱ）解：因为AC⊥BC，且DE⊥AC，所以BC∥DE．
所以四边形CMDE为平行四边形，所以CE=MD，（6分）
由
=
，设AC=3x，AB=5x，则OM=
x，
又OD=
x，所以MD=
x-
x=x，
所以AE=AC+CE=4x，
因为OD∥AE，所以
=
=
=
．（10分）
因为OA=OD，所以∠OAD=∠ODA，（2分）
又因为∠OAD=∠DAE，所以∠ODA=∠DAE，
所以OD∥AE．（4分）
（Ⅱ）解：因为AC⊥BC，且DE⊥AC，所以BC∥DE．
所以四边形CMDE为平行四边形，所以CE=MD，（6分）
由
| AC |
| AB |
| 3 |
| 5 |
| 3 |
| 2 |
又OD=
| 5 |
| 2 |
| 5 |
| 2 |
| 3 |
| 2 |
所以AE=AC+CE=4x，
因为OD∥AE，所以
| AF |
| FD |
| AE |
| OD |
| 4x | ||
|
| 8 |
| 5 |
点评：本题考查直线与直线平行的证明，考查两线段比值的求法，是中档题，解题时要认真审题，注意圆的简单性质的合理运用．
练习册系列答案
相关题目
已知函数f（x）=axsinx-
（a＞0）在（
，π）内有两个零点，则a的可能值为（ ）
| 3 |
| 2 |
| π |
| 2 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|