题目内容
函数f(x)=cos3x+sin2x-cosx在[0,2π)上的最大值为 .
考点:三角函数的最值
专题:导数的综合应用,三角函数的求值
分析:令cosx=t,由 x∈[0,2π),可得-1≤t≤1,f(x)=g(t)=(1-t2) (1-t),再利用导数研究函数的单调性,由函数的单调性求得函数的最值.
解答:
解:函数f(x)=cos3x+sin2x-cosx=cos3x+1-cos2x-cosx=(1-cos2x)(1-cosx).
令 cosx=t,∵x∈[0,2π),可得-1≤t≤1,f(x)=g(t)=(1-t2)(1-t),
∴g′(t)=3t2-2t-1.
令g′(t)=0,求得t=1,或t=-
.
再根据导数的符号可得g(t)的增区间为[-1,-
],减区间为(-
1].
故当t=-
时,函数g(t)取得最大值为
.
故答案为:
.
令 cosx=t,∵x∈[0,2π),可得-1≤t≤1,f(x)=g(t)=(1-t2)(1-t),
∴g′(t)=3t2-2t-1.
令g′(t)=0,求得t=1,或t=-
| 1 |
| 3 |
再根据导数的符号可得g(t)的增区间为[-1,-
| 1 |
| 3 |
| 1 |
| 3 |
故当t=-
| 1 |
| 3 |
| 32 |
| 27 |
故答案为:
| 32 |
| 27 |
点评:本题主要考查利用导数研究函数的单调性,由函数的单调性求函数的最值,属中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
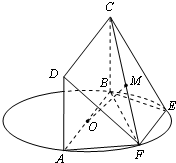
 在多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2AB,F为棱CE上异于点C、E的动点,则下列说法正确的有( )
在多面体ABCDE中,AB⊥平面ACD,DE⊥平面ACD,AC=AD=CD=DE=2AB,F为棱CE上异于点C、E的动点,则下列说法正确的有( )①直线DE与平面ABF平行;
②当F为CE的中点时,BF⊥平面CDE;
③存在点F使得直线BF与AC平行;
④存在点F使得DF⊥BC.
| A、1个 | B、2个 | C、3个 | D、4个 |
在区间[-
,
]上随机取一个数x,则cosπx的值介于
与
之间的概率为( )
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知i是虚数单位,m和n都是实数,且m(1+i)=
+m,则(
)2015=( )
| 3 |
| m+ni |
| m-ni |
| A、-1 | B、1 | C、-i | D、i |
 如图,AB为圆O的直径,四方形ABCD为正方形,点E,F在圆O上,AD⊥AF,AB=AF=2.
如图,AB为圆O的直径,四方形ABCD为正方形,点E,F在圆O上,AD⊥AF,AB=AF=2.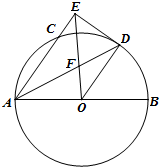 如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若
如图,已知AB是⊙O的直径,AC是⊙O的弦,∠BAC的平分线AD交⊙O于D,过点D作DE⊥AC交AC的延长线于点E,OE交AD于点F.若